Производная от неявно заданной функции нескольких переменных

[Gecko]

Утундрий в сообщении #1428474 писал(а):

но есть второй вариант.

Можно поподробнее?

[arseniiv]

Gecko
А перемножьте-ка их в обратном порядке, по-моему тут перепуталось.

-- Пн дек 02, 2019 02:30:31 --

Ну да, в обычном определении дифференцируемая функция меняется по строкам, а то, по чему дифференцируют, по столбцам. Тогда если $A^i{}_j = \frac{\partial f^i}{\partial g^j}$ и $B^i{}_j = \frac{\partial g^i}{\partial h^j}$, для произведения получаем $(AB)^i{}_k = \sum_j \frac{\partial f^i}{\partial g^j} \frac{\partial g^j}{\partial h^k} = \frac{\partial f^i}{\partial h^k}$, всё правильно умножилось и сложилось.

P. S. Добавил знак суммирования для тех, кто не в курсе индексной тензорной записи. Замечательной, прекрасной.

-- Пн дек 02, 2019 02:34:05 --

Утундрий в сообщении #1428353 писал(а):

то есть определителей вида

Плюс тут ведь достаточно матриц Якоби, зачем сразу определители. С определителями как раз наверно будет не очень понятно, что происходит, да и из тождества для матриц тождество для них уже выведем.

[Утундрий]

Поскольку нас в конечном итоге интересуют детерминанты, то матрицы можно ещё и транспонировать.

-- Пн дек 02, 2019 01:37:25 --

arseniiv в сообщении #1428478 писал(а):

тут ведь достаточно матриц Якоби, зачем сразу определители

Кстати, да. Куда-то меня не туда затянуло. Всё обломалось в доме Смешанских...

[arseniiv]

Вообще ваше транспонированное определение как раз удобнее, если мы захотим применять матрицы к столбцу (более распространено), а не к строке (менее; эти и многие другие комментарии все для ТС), как с обычным. Но порядок умножения будет аналогичен тому, который в обозначении композиции функций, с мнемоникой не «$A$, затем $B$», а «$A$ после $B$».

Кроме того оно удобнее тем, что можно писать у $f_i, g_i, h_i$ обычные нижние индексы и не поступиться соглашением о различии верхних и нижних — они будут полностью оправданы.

[Утундрий]

А, вспомнил! Зачем определители. Пуркуа

$$\[ \frac{{\partial a}} {{\partial x}} = \frac{{\partial \left( {a,y} \right)}} {{\partial \left( {x,y} \right)}}, \qquad \frac{{\partial a}} {{\partial y}} = \frac{{\partial \left( {x,a} \right)}} {{\partial \left( {x,y} \right)}} \] $$

[Gecko]

arseniiv в сообщении #1428478 писал(а):

Gecko
А перемножьте-ка их в обратном порядке, по-моему тут перепуталось.

$\begin{pmatrix} _\dfrac{\partial a}{\partial x}& _\dfrac{\partial b}{\partial x} \\ _\dfrac{\partial a}{\partial y}& _\dfrac{\partial b}{\partial y} \end{pmatrix} \cdot \begin{pmatrix} _\dfrac{\partial f}{\partial a}& _\dfrac{\partial h}{\partial a} \\ _\dfrac{\partial f}{\partial b}& _\dfrac{\partial h}{\partial b} \end{pmatrix} = \begin{pmatrix} _\dfrac{\partial a}{\partial x}\dfrac{\partial f}{\partial a}+\dfrac{\partial b}{\partial x}\dfrac{\partial f}{\partial b}& _\dfrac{\partial a}{\partial x}\dfrac{\partial h}{\partial a}+\dfrac{\partial b}{\partial x}\dfrac{\partial h}{\partial b} \\ _\dfrac{\partial a}{\partial y}\dfrac{\partial f}{\partial a}+\dfrac{\partial b}{\partial y}\dfrac{\partial f}{\partial b}& _\dfrac{\partial a}{\partial y}\dfrac{\partial h}{\partial a}+\dfrac{\partial b}{\partial y}\dfrac{\partial h}{\partial b} \end{pmatrix}$

Что-то легче не становится...

[Pphantom]

Gecko в сообщении #1428644 писал(а):

Что-то легче не становится...

Почему же? Присмотритесь к элементам матрицы в правой части равенства внимательнее.

[Otta]

arseniiv в сообщении #1428478 писал(а):

А перемножьте-ка их в обратном порядке, по-моему тут перепуталось.

Нет, порядок правильный. Неверно составлена матрица, перепуталось тут:

Утундрий в сообщении #1428353 писал(а):

$$\[ \frac{{\partial \left( {a,b} \right)}} {{\partial \left( {x,y} \right)}} \enskip \equiv \enskip \left| {\begin{array}{*{20}c} {\dfrac{{\partial a}} {{\partial x}}} & {} & {\dfrac{{\partial b}} {{\partial x}}} \\ {} & {} & {} \\ {\dfrac{{\partial a}} {{\partial y}}} & {} & {\dfrac{{\partial b}} {{\partial y}}} \\ \end{array} } \right| \] $$

обладающих удобным свойством

$$\[ \frac{{\partial \left( {f,h} \right)}} {{\partial \left( {a,b} \right)}} \cdot \frac{{\partial \left( {a,b} \right)}} {{\partial \left( {x,y} \right)}} = \frac{{\partial \left( {f,h} \right)}} {{\partial \left( {x,y} \right)}} \] $$

.

Надо:

$$\[ \frac{{\partial \left( {a,b} \right)}} {{\partial \left( {x,y} \right)}} \enskip \equiv \enskip \left[ {\begin{array}{*{20}c} {\dfrac{{\partial a}} {{\partial x}}} & {} & {\dfrac{{\partial a}} {{\partial y}}} \\ {} & {} & {} \\ {\dfrac{{\partial b}} {{\partial x}}} & {} & {\dfrac{{\partial b}} {{\partial y}}} \\ \end{array} } \right] \] $$

А вот теперь надо выписать правую и левую части, все перемножив, где требуется.

[arseniiv]

Otta
Да, «тут перепуталось» больше относилось к определению, чем к формуле для умножения, хотя я выше там нашёл неплохой аргумент (две штуки) в пользу как раз такого непривычного определения.

[Gecko]

Otta в сообщении #1428647 писал(а):

Надо:

$$\[ \frac{{\partial \left( {a,b} \right)}} {{\partial \left( {x,y} \right)}} \enskip \equiv \enskip \left[ {\begin{array}{*{20}c} {\dfrac{{\partial a}} {{\partial x}}} & {} & {\dfrac{{\partial a}} {{\partial y}}} \\ {} & {} & {} \\ {\dfrac{{\partial b}} {{\partial x}}} & {} & {\dfrac{{\partial b}} {{\partial y}}} \\ \end{array} } \right] \] $$

А вот теперь надо выписать правую и левую части, все перемножив, где требуется.

О, вот так мне стало ясно! Спасибо.

-- 02.12.2019, 23:50 --

Pphantom в сообщении #1428646 писал(а):

Gecko в сообщении #1428644 писал(а):

Что-то легче не становится...

Почему же? Присмотритесь к элементам матрицы в правой части равенства внимательнее.

У меня просто сомнения насчет того, что

$\dfrac{\partial a}{\partial x}\dfrac{\partial f}{\partial a}=\dfrac{\partial f}{\partial a}\dfrac{\partial a}{\partial x}$

-- 02.12.2019, 23:56 --

Хотя какие могут быть сомнения? Так оно и есть!

[Утундрий]

Где бы эти детерминанты могли пригодиться? Пусть, например, дан принцип

$$\delta \int\limits_1^2 {L\left( {x,\dot x} \right)dt} = 0$$

приводящий к уравнениям $\dot p = L_x $, где обозначено $p: = L_{\dot x} $. Сделаем замену

$$\left\{ {\begin{array}{*{20}c} {q &=& x} \\ {p &=& L_{\dot x} \left( {x,\dot x} \right)} \\ \end{array} } \right.$$

и вычислим её якобиан

$$\frac{{\partial \left( {q,p} \right)}}{{\partial \left( {x,\dot x} \right)}} = \left| {\begin{array}{*{20}c} 1 & 0 \\ {} & {L_{\dot x\dot x} } \\ \end{array} } \right| = L_{\dot x\dot x} $$

Если $L_{\dot x\dot x} \ne 0$, то перед нами таки замена переменных и всё можно выразить взад

$$\left\{ {\begin{array}{*{20}c} {x &=& q} \\ {\dot x &=& v\left( {q,p} \right)} \\ \end{array} } \right. $$

Теперь возьмём интеграл $E: = \dot xL_{\dot x} - L = const$ и посмотрим на него как на функцию $q$ и $p$:

$$H\left( {q,p} \right): = \left. E \right|_{x=q,\dot x = v\left( {q,p} \right)} = v\left( {q,p} \right)p - \left. L \right|_{x=q,\dot x = v\left( {q,p} \right)} $$

Отыщем её первые частные производные не экономным общепринятым методом, а извращенски через якобианы.

$$\[ \frac{{\partial H}} {{\partial q}} = \frac{{\partial \left( {H,p} \right)}} {{\partial \left( {q,p} \right)}} = \frac{{\partial \left( {x,\dot x} \right)}} {{\partial \left( {q,p} \right)}}\frac{{\partial \left( {H,p} \right)}} {{\partial \left( {x,\dot x} \right)}} = \frac{1} {{L_{\dot x\dot x} }}\frac{{\partial \left( {E,L_{\dot x} } \right)}} {{\partial \left( {x,\dot x} \right)}} = \frac{1} {{L_{\dot x\dot x} }}\left| {\begin{array}{*{20}c} {\dot xL_{\dot xx} - L_x } & {\dot xL_{\dot x\dot x} } \\ {L_{x\dot x} } & {L_{\dot x\dot x} } \\ \end{array} } \right| = - L_x = - \dot p \] $$

$$\[ \frac{{\partial H}} {{\partial p}} = \frac{{\partial \left( {q,H} \right)}} {{\partial \left( {q,p} \right)}} = \frac{{\partial \left( {x,\dot x} \right)}} {{\partial \left( {q,p} \right)}}\frac{{\partial \left( {q,H} \right)}} {{\partial \left( {x,\dot x} \right)}} = \frac{1} {{L_{\dot x\dot x} }}\frac{{\partial \left( {x,E} \right)}} {{\partial \left( {x,\dot x} \right)}} = \frac{1} {{L_{\dot x\dot x} }}\left| {\begin{array}{*{20}c} 1 & 0 \\ {} & {\dot xL_{\dot x\dot x} } \\ \end{array} } \right| = \dot x = \dot q \] $$

То есть

$${\dot p = - \frac{{\partial H}}{{\partial q}}, \quad \dot q = \frac{{\partial H}}{{\partial p}}}$$

Упражнение Проделать всё то же для системы с действием

$$\int {L\left( {x,\dot x,\ddot x} \right)} dt$$

[Someone]

Gecko в сообщении #1428337 писал(а):

$\dfrac{\partial w}{\partial x}=\dfrac{\partial w}{\partial x}+\dfrac{\partial w}{\partial u}\dfrac{\partial u}{\partial x}$

Вот здесь непонятно. Смущает такая запись. Ведь $ \dfrac{\partial w}{\partial x}$ в левой и правой части уравнения - это разные вещи.

Тут банально не хватает обозначений. В левой части имеется в виду "полная" производная по $x$, а в правой — "частная" производная по (явному вхождению) $x$: $\dfrac{\partial w}{\partial x_{\text{полн.}}}=\dfrac{\partial w}{\partial x_{\text{явн.}}}+\dfrac{\partial w}{\partial u}\dfrac{\partial u}{\partial x}$.

[arseniiv]

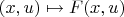
О, ту вещь пропустил. Я бы сказал, не стоит обозначать две разные функции как $w$. Левая $w$ в формуле — это $(x, y)\mapsto F(x, f(x, y))$, а правая $w$ — $(x, u)\mapsto F(x, u)$, ну или просто $F$ — и в вычислении производной я бы первую $w$ оставил как есть, раз никакого короткого обозначения у неё не получится, а вместо второй написал бы законную $F$, раз уж ей уже дали имя. Лучше бы им обеим дали имена как следует, а не только в виде букв, обозначающих выражения или переменные (как в случае с $u$).

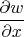
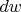
Но кстати говоря помнится, что классически вместо левого вхождения $\dfrac{\partial w}{\partial x}$ вроде рекомендуется писать $\dfrac{dw}{dx}$, именно чтобы не путать, где мы взяли частную производную, а где взяли пропорциональную $dx$ часть $dw$. Хотя это наверно не лучшее обозначение, потому что вот делением дифференциалов это как раз не будет — кроме редкого случая, когда большая функция в итоге имеет лишь один аргумент, по которому и дифференцируется, а в этой теме например их два.

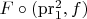
Если бы все тексты по производной хитрой композиции функций описывали всё прозрачно, либо вводя имена для всех функций, от которых берутся производные в формуле, либо записывая композицию как-нибудь явно, например как $F\circ(\mathrm{pr}_1^2, f)$, было бы наверно не в пример лучше. А так это одно из мест, где какая-то доля людей постоянно спотыкается, насколько я вижу. Хотя на деле все трудности не в каких-нибудь тайных закоулках производной композиции функций, а в лени авторов курса написать лишнюю пару букв и слов.

Если подумать, вообще раз мы говорим о производных композиции, стоило бы сначала разобраться во всех тех видах композиции, которые должны охватываться формулой этой производной. То есть если вместо многих аргументов функции подставляются значения функций в свою очередь многих аргументов, это как минимум стоило бы сначала отдельно попробовать на язык и убедиться, что обозначения однозначные и пр.. Насколько люди со мной согласятся? (Да, это казалось бы такая мелочь, но темы периодически производит. Всё очевидное кому-то неизвестно, как обычно, и не всегда верно.)

[Утундрий]

Я бы ещё упомянул каким-то чудом не упомянутую "термодинамическую" нотацию

$$\frac{{\partial f(x,y,z)}} {{\partial x}} \equiv \left( {\frac{{\partial f}}{{\partial x}}} \right)_{y,z} $$

[arseniiv]

В такие воды заходить (в этой теме и на мой взгляд) опасно, потому что там-то величины уже не функции, а просто координаты точек некоторой поверхности, так что мы можем иметь шесть разных определённых не обязательно нулевых величин $p'_T, p'_V, V'_p, V'_T, T'_p, T'_V$. А в случаях как тут функции заданы раз и навсегда и всё куда проще, ничего страшнее композиций, никаких неявных заданий, никакого обращения с вольным именованием обратной функции и её аргумента старыми буквами наоборот.