e]Вам теорию или практику? В теории всё обратимо, на практике всё необратимо. На практике мы можем отмотать назад тысячи циклов вращения планет солнечной системы, основываясь на их современных координатах и скоростях. Потому что они движутся по устойчивым траекториям. Но не можем отмотать десятки соударений диска в бильярде Синая, потому что там неустойчивые траектории, как бы мы точно всё не измеряли.
"Необратимые процессы в физических моделях", тобишь в физических абстракциях, тобишь никакой реальности не существует, что логично, ведь речь идет
только об моделях.
Но мы можем легко отмотать этот биллиард Синая
в модели, по крайней мере с того что я понял можем, ибо в этой абстракции мы
идеально точно знаем и функцию состояний и сами состояния в какой-то начальный момент времени, а дальше дело техники, есть же там какая-то теория которая, там говорит что в общем случае имеются какие-то там решения в каком-то там виде, верно? То есть уровень обобщения, абстракции, как точно эти абстракции описывают реальность — вопрос совсем иной.
А вот когда мы говорим о моделе Вселенной, то не можем отмотать в общем случае, ибо мы всегда можем сказать что
система открытая, это походу и подразумевал мистер Шелепин в своей книге!
Типа того.
Ура!
Если мы замкнутую рассмотрим систему из

частиц, то она описывается

уравнениями (для простоты - пусть это уравнения классической механики). Эти уравнения обратимы - замена

на

не меняет вида уравнений, значит все процессы могут идти как в одну сторону, так и в другую. Вместо уравнений механики можно написать уравнения на вероятность найти любую частицу в токе

вероятность найти какую-то частицу в точке

а другую - в точке

и т.д.
Заменяя уравнения класической механики на вероятностные штуки, мы подразумеваем что нету например
абсолютно никакой связи между координатами и импульсами (пусть массы там будут нескольких видов или у всех элемнтов одинаковая масса, но не бесконечное количество разновидностей...), то есть включаем хаос? Для меня сам факт что такие уравнения могут быть эквивалентны исходным удивителен и невообразим даже! Наверное есть какая-то сложная, сильно абстрактная математика по этому поводу.
e]Что бы такие уравнения были эквивалентны исходным, их, по крайней мере, должно быть столько же, сколько исходных уравнений механики. Решить эту систему из

уравнений невозможно, поэтому мы берем в руки шаманский бубен и произносим следующее заклинание. Многочастичная функция распределения означает, что есть жесткая корреляция между движением разных частиц. Однако, замкнутых систем не бывает, всегда есть неконтролируемое взаимодействие с окружением. Это взаимодействие разрушает корреляцию, причем чем больше частиц - тем легче такая корреляция разрушается. Поэтому мы оборвем получившуюся цепочку, сказав, что, скажем, трехчастичная функция выражается через одно и двухчастичные. После этого бубен откладывается, и решается получившееся уравнение (уравнение Больцмана). Удивительным образом, результат совпадает с экспериментом.
Это божественно гениально! Как там в книги этой, этих ученых называли, Боголюбов, Борн, Грин, Кирквуд, Ивон, поэтому метод "ББГКИ", как они до такой штуки додумались?! Тут задачку простую, школьную, бывает попомучаешься пока решишь...
Многочастичная функция распределения состояний во времени? Жесткая корреляция между движения разных частиц? — Это потому-что у нас всегда будет в цепочке решений какое-то

для одной частицы? То есть уравнение пусть будет

, тогда:
Где

— это совокупность свойств элемента системы, типа координата, импульс, так далее... Но поскольку вот, насколько я понял
математика говорит что эта многочастичная, такая-эдакая штука есть, то в следствии есть
жесткая зависимость этих

, соответственно нарушение этой зависимости будет в открытой системе тем больше чем больше количество частиц

и чем дальше во времени от какого-то начального момента, допустим
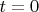
, есть в открытой системе мы можем представить это как закрытую систему, и приписать какое-то там

, грубо говоря, и тогда чем дальше оно по цепочке (или времени) от

, тем катастрофичней нарушается эта жесткая корреляция! То есть система складывается с огромной кучи элементов и достаточно далеко от начального момента когда там нам известны в явном виде все эти свойства, их совокупность то есть состояние, тогда мы можем, допустим, сказать что:
И таким образом у нас не

уравнений а только три! Невероятно, действительно невероятно! Как такая ужасная апроксимация угадывает реальность, если оно действительно угадывает достаточно точно, кончено.
Вообще, эта теория хаоса напоминает мою манеру самообучения-повторения, никакой системности, и бог знает что впереди будет...

Поэтому если я нонсенс напечатал, то не обращайте внимания, я только в тоненькой, научно-популярной книжечке о методе ББГКИ почитал.