Someone писал(а):
Сорокин Виктор писал(а):
1) множества

и

простых сомножителей в обеих частях равенства Ферма тождественно равны (и Вы с этим согласны);
СЛЕДОВАТЕЛЬНО
2) множества

и


-значных окончаний этих сомножителей в обеих частях равенства тоже равны (поскольку у каждого простого сомножителя

-значное окончание ЕДИНСТВЕННО) (и с этим Вы тоже как будто согласны) [замечу, в последующем анализе цифры бОльших разрядов нам не понадобятся, и они полностью игнорируются];
Ну, в силу основной теоремы арифметики

и, следовательно,

. Вообще-то, я употребляю Вашу терминологию, но морщусь при этом. Поскольку речь идёт не о множествах простых сомножителей, а о разложениях чисел на простые множители. Ну Бог с Вами.
Ваша терминология не подходит мне по существу: ведь я анализирую

-значные окончания, и не существует

-значного числа, которое разлагается на простые сомножители, множество которых совпадает с множеством всех

-значных окончаний в левой или правой части равенства. Конечно, можно удовлетворить и Вашему желанию: в левой части равенства все простые сомножители разбить на

равных подмножеств (каждое из которых составляет число а), а в правой части на два неравных (и взаимопростых) сомножителя –

и

, но НЕ ЗАБЫВАЯ при этом, что сумма разложений этих чисел разбиваема на

равных подмножеств. После этого мы в каждом простом сомножителе (в левой и правой частях равенства) ОСТАВЛЯЕМ ТОЛЬКО

-значные окончания, поскольку цифры старших разрядов НИ КОИМ ОБРАЗОМ НЕ УЧАСТВУЮТ в формировании в каждой части равенства по

РАВНЫХ множеств

-значных окончаний, и мы имеем полное право КАК УГОДНО поменять местами простые сомножители в правой части равенства. И вот в результате выгодной нам перестановки

-значное окончание каждого из

равных произведений (в правой части равенства) равно

. И никакая иная перестановка простых сомножителей – при условии РАВЕНСТВА множеств в

произведениях

-значных окончаний – изменить это значение, т.е.

, НЕ МОЖЕТ.
Someone писал(а):
Сорокин Виктор писал(а):
СЛЕДОВАТЕЛЬНО
3) оба новых множества (т.е. ОКОНЧАНИЙ, а НЕ чисел) разбиваемы на n равных (во всех отношениях) подмножеств {

} и {

} (поскольку на n равных подмножеств разбиваем равных множества P и T;
Someone писал(а):
Здесь уже возникает неоднозначность разбиения, поскольку
различные простые множители числа

могут иметь
одинаковые 
-значные окончания. И такие простые множители можно перетаскивать из одной части разбиения в другую, заменяя
другим множителем с таким же окончанием. Множества окончаний останутся при этом "равными", но соответствующие им множества простых сомножителей (и соответствующие произведения) равными не будут.
Да, множества простых сомножителей – если их перераспределить при условии равенства

подмножеств – будут не равны. Но меня это совершенно не интересует. Ведь когда я анализирую

-значные окончания, то я вообще могу отбросить все головные части чисел, поскольку на обнаруженое противоречие они никак повлиять не могут. Таким образом, неоднозначность есть, но она находится не "внутри" доказательства, а где-то рядом, никак не касаясь ОДНОЗНАЧНОСТИ разбиения

-кратного множества на

равных частей..
Someone писал(а):
Сорокин Виктор писал(а):
СЛЕДОВАТЕЛЬНО
4) произведение всех чисел

и произведение всех ТАКИХ ЖЕ чисел

должны быть РАВНЫ по ВСЕМ цифрам.
Ну, равными обязаны быть только

-значные окончания этих произведений. Причём, в рассматриваемом нами примере (

) они однозначно будут

, а не

, как Вам хочется, поскольку замена одного сомножителя другим с таким же

-значным окончанием не влияет на

-значное окончание произведения.
Someone писал(а):
Нет, именно по всем цифрам этих двух чисел, поскольку они состоят из одних и тех же сомножителей.
Сорокин Виктор писал(а):
Однако для доказательства противоречия нам достаточно сравнить лишь

-е цифры у этих произведений, которые как раз и оказываются НЕРАВНЫМИ.
Видите ли, Вы пока что
не предъявили разбиения множества

на
 равных
равных частей

, произведения которых оканчивались бы на

. Всё, что Вы смогли - это разбить множество

на
два подмножества, произведения которых оканчиваются на

. Поэтому говорить о противоречии
рано.
Заметим, что старшие цифры в анализе не участвуют и оба подмножества состоят из

-значных окончаний. И соотношение 4° говорит как раз о том, что второй из интересующих нас сомножителей есть

-кратное повторение первого сомножителя – по меньшей мере когда первый сомножитель равен

.
Someone писал(а):
Правда, Вы доказывали, что числа

и

имеют одинаковые

-значные окончания. Ну и что? Эти числа имеют
различные разложения на простые множители. В эти разложения входят
различные простые числа, количества этих чисел
различны,

-значные окончания этих простых чисел также
различны. Мы не можем установить никакого соответствия между простыми сомножителями чисел

и

, поэтому возможность разбиения множества
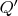

-значных окончаний простых сомножителей числа

на

равных частей

абсолютно ничего не даёт для множества

.
[/quote]
Еще раз: я не "установливаю никакого соответствия между простыми сомножителями чисел

и

" – мне это совершенно не нужно. Я устанавливаю соответствие между ОКОНЧАНИЯМИ этих чисел. И, полагаю, мне это удалось вполне.