Переходные процессы в катушке индуктивности.

[wrest]

jast321 в сообщении #1325430 писал(а):

Скажите, как только разомкнули ключ, будет ли ток через эти два резистора и катушку равняться 1А или он будет меньше?

Принято говорить что будет равняться.
Вот у вас в руке гиря, она покоится. "Как только" вы ее отпустили -- она еще покоится или уже немножко двигается? Обычно подразумевают что еще покоится (скорость равна нулю). Но вот уже ускорение, "как только отпустили" меняется мгновенно, то есть сразу становится равным ускорению свободного падения.

[jast321]

DimaM в сообщении #1325431 писал(а):

jast321 в сообщении #1325430 писал(а):

Скажите, как только разомкнули ключ, будет ли ток через эти два резистора равняться 1А?

Разумеется. Причем даже если резисторы не равны.

Вот тут мне и не понятно. Смотрите, чтобы через два резистора протек ток такой же величины как до выключения необходимо увеличить напряжение.
Напряжение увеличиться из-за изменения магнитного потока.
Если магнитный поток уменьшился, то и $B$ тоже уменьшилось. Но ведь $B$ пропорционально току. Значит ток должен стать меньше, чем тек до выключения. Да, можен на это и нужно какой то очень короткий момент времени..

[realeugene]

DimaM в сообщении #1325431 писал(а):

Дальше будет затухать экспоненциально с характерным временем $\tau=L/(R_1+R_2)$.

Дальше зависимость тока от времени будет $I(t)=I_0 e^{-t/\tau}$

-- 09.07.2018, 15:20 --

jast321 в сообщении #1325434 писал(а):

Напряжение увеличиться из-за изменения магнитного потока.

Чему при этом будет равно напряжение?

Если вы спрыгнете с табуретки, то в первый момент времени вы зависнете на высоте табуретки. Падая при этом.

[DimaM]

jast321 в сообщении #1325434 писал(а):

Напряжение увеличиться из-за изменения магнитного потока.
Если магнитный поток уменьшился, то и $B$ тоже уменьшилось.

Как выше уже намекали, напряжение пропорционально производной тока (как ускорение есть производная скорости). Ток, конечно, будет уменьшаться, но в самый первый момент останется практически таким же.

[Cos(x-pi/2)]

(как всегда я опаздываю, но пусть будет и этот пост раз уж напечатал)

jast321
Продифференцировать $W=\frac{1}{2}LI^2$ по времени и тем самым получить формулу для скорости $\frac{dW}{dt}$ ухода энергии из катушки нам с Вами необходимо суметь! Если, конечно, не перепрыгивать на новое, а продолжать спокойно и последовательно разбирать уже начатое и следовать вот такому плану:

Мы ведь знаем, что (по закону сохранения энергии) энергия из катушки не может уходить в никуда; она должна куда-то поступать. Мы также знаем про эффект Джоуля и Ленца: если через резистор течёт ток, то резистор греется. Т.е. в резистор с током поступает энергия (она становится добавкой к энергии теплового движения молекул в веществе резистора, и затем от резистора передаётся молекулам окружающего воздуха, то есть в итоге поступает в виде тепла в окружающую среду). Наверное, Вы знаете формулу для скорости выделения тепла в резисторе с током; другими словами говоря, - знаете формулу для мощности $P,$ потребляемой резистором $R,$ когда по нему течёт ток $I.$

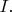
На схеме с разомкнутым ключом (нижняя схема на моём рисунке) видна как раз такая картина: через резистор $R$ течёт ток $I(t),$ тот же самый, что и в катушке; а цепь с батарейкой не при делах - она разомкнута. Значит, пока ток в катушке не равен нулю, резистор греется. Причём, как видно на схеме с разомкнутым ключом, мощность $P$ в резистор может поступать только из катушки - больше неоткуда. И значит, следует приравнять мощность $-\frac{dW}{dt},$ уходящую из катушки, к мощности $P,$ поступающей в резистор $R:$

$-\dfrac{dW}{dt} = P.$

В левой и правой части здесь будут выражения, содержащие $I$ и $\frac{dI}{dt},$ и тем самым получится уравнение для пока неизвестной нам функции $I(t),$ т.е. это будет уравнение для зависимости тока в катушке от времени (при разомкнутом ключе).

Решив его, мы и узнаем, как ведёт себя ток $I(t).$ И тогда при желании даже можно будет построить, разглядеть и обдумать график $I(t).$ Затем можно будет подставить найденную функцию $I(t)$ в формулу энергии катушки, и тем самым узнать, как именно изменяется энергия катушки $W(t)$ со временем. И будет видно, как именно меняется со временем напряжение на резисторе $U(t)=I(t)R,$ которое является и напряжением на выводах катушки. И будет видно, как именно в катушке меняется со временем магнитный поток $\Phi (t)=LI(t).$ То есть - мы узнаем всё!

Это я хотел бы ещё раз подчеркнуть: физическая картина, как видите, выясняется не сочинением словесных формулировок, а количественным анализом явлений! Потому что физические явления, как показывает опыт, подчиняются количественным закономерностям. Почему физические явления законопослушны столь удивительным образом, люди не знают; но это твёрдо установленный факт.

Результаты количественного анализа, когда они уже получены и поняты, в дальнейшем можно формулировать краткими фразами, для удобства запоминания. Но обратное, т.е. - заучивание формулировок (типа "катушка пытается сохранить ток", "энергия пропадает резко", и т.п.) без применения количественных законов - это путь к непониманию.

jast321 в сообщении #1325402 писал(а):

У меня среднее образование. И то очень много подзабыл.

Ах, вот оно как; извините, я не знал...

jast321, среднего образования, да ещё и подзабытого, конечно, маловато... Тогда тут два пути: либо забить на заведомо обречённых попытках хорошо понять физику без достаточного образования... Либо всё-таки повышать свой уровень знаний и не избегать необходимой математики.

Не знаю, каким будет Ваш выбор. На всякий случай предложу ещё вопрос (но, конечно, ни к чему Вас не обязываю). Допустим, Вас не учили "дифференцировать функции". Однако не так уж сложно проделать действия, знакомые из школьной алгебры. Попробуем сначала получить выражение для изменения энергии катушки $dW,$ исходя из того, что в какой-то конкретный момент времени $t$ ток имеет конкретную величину $I,$ а в более поздний момент $t+dt$ ток уже изменился на $dI$ и равен $I+dI.$

Тогда энергия катушки в момент $t$ равна $\frac{1}{2}LI^2,$ а в момент $t+dt$ она равна $\frac{1}{2}L(I+dI)^2.$ Разность этих двух значений энергии и есть изменение энергии $dW$ за время $dt:$

$dW\,=\, \frac{1}{2}L(I+dI)^2 \,-\, \frac{1}{2}LI^2.$

Если решили пока "не забивать" на выкладках, то попробуйте раскрыть здесь $(I+dI)^2$ и выписать, что получилось для такого $dW.$

[wrest]

jast321 в сообщении #1325434 писал(а):

Смотрите, чтобы через два резистора протек ток такой же величины как до выключения необходимо увеличить напряжение.
Напряжение увеличиться из-за изменения магнитного потока.

Вот это "из-за" вам и мешает :)
Вообще, если вы попробуете разомкнуть хорошую катушку по которой до размыкания протекал ток, то может неслабо так шарахнуть, потому что ток потечет уже не по проводам а через воздух, и напряжение будет киловольты. Если при этом размыкаемые концы будут у вас в руках, то ток потечет через вас, что может причинить довольно неприятные ощущения, а то и того... в море...

[Dmitriy40]

(Замечание в сторону, ТС не читать!)

Интересно, а ведь можно прикинуть максимально возможное напряжение на выводах катушки при размыкании тока, оно ж не может превысить количества дрейфующих электронов. Да, число Авогадро огромно, но не бесконечно. Да и нарастающее электрическое поле будет препятствовать нарастанию напряжения (и думаю заборет ток задолго до числа Авогадро). Прикинуть бы реализуемость такой "сверхкатушки" с реальным изолятором, тончайшим проводом и микротоком, можно ли реально обнаружить эффект ограничения напряжения или он весь съестся зарядом ёмкости конструкции ... или её всё же можно сделать незначительной ... Забавный вопрос, наверное для олимпиадного раздела подойдёт.
Хм, а это вообще возможно из принципов электротехники без привлечения электродинамики и рассмотрения распространения ЭМ волн по катушке? Что-то даже засомневался.

[jast321]

realeugene в сообщении #1325437 писал(а):

Чему при этом будет равно напряжение?

Если вы спрыгнете с табуретки, то в первый момент времени вы зависнете на высоте табуретки. Падая при этом.

Ну так в первый момент времени для поддержания такого же тока оно должно быть ровно а два раза больше (если резисторы одинаковы) и тогда на каждом из резисторов будет такое же напряжение, как до отключения.

[wrest]

jast321 в сообщении #1325453 писал(а):

Ну так в первый момент времени для поддержания такого же тока оно должно быть ровно а два раза больше (если резисторы одинаковы).

Да, оно и станет в два раза больше. Мгновенно. Или в 100 раз больше, в зависимости от шунтирующего сопротивления $R_2$ по вашей схеме, чем оно больше тем больше будет ток.

Но вот есть еще такие штуки как конденсаторы. У них наоборот, напряжение не может поменяться скачком. А ток - может. Поэтому когда вы заряженный конденсатор замыкаете, напряжение в первый момент сохраняется, а ток многократно растет (т.к. падает сопротивление). Но результат похож: биг-бада-бум, если конденсатор емкий.

Можно замкнуть заряженный конденсатор на катушку. Тогда выполнятся оба условия: в первый момент напряжение будет такое как было на конденсаторе до подключения катушки, а ток будет такой как был в катушке до подключения её к конденсатору (нулевой). И начнется колебательный процесс...

[jast321]

wrest в сообщении #1325455 писал(а):

Да, оно и станет в два раза больше. Мгновенно. Или в 100 раз больше, в зависимости от шунтирующего сопротивления $R_2$ по вашей схеме, чем оно больше тем больше будет ток.

Извините, я наверное сейчас повторяюсь, но вследствии чего напряжение выростает в несколько раз? Вследствии изменения магнитного потока в катушке. Верно?

[realeugene]

jast321 в сообщении #1325461 писал(а):

Извините, я наверное сейчас повторяюсь, но вследствии чего напряжение выростает в несколько раз? Вследствии изменения магнитного потока в катушке. Верно?

Нет, неверно. Напряжение возрастает в несколько раз вследствие уравнений Максвелла и резкого возрастания сопротивления внешней цепи. На внешней цепи при том же протекающем токе падает большее напряжение

[wrest]

jast321 в сообщении #1325461 писал(а):

Извините, я наверное сейчас повторяюсь, но вследствии чего напряжение выростает в несколько раз? Вследствии изменения магнитного потока в катушке. Верно?

Нет, не верно. Магнитный поток в первый момент ("как только разомкнули") остается тем же, что был в момент до размыкания, а значит остается той же и сила тока.
По закону Ома $U=IR$, $I$ у нас в первый момент константа, а $R$ возрастает в два раза, значит и $U$ возрастает в два раза.

[jast321]

realeugene в сообщении #1325465 писал(а):

jast321 в сообщении #1325461 писал(а):

Извините, я наверное сейчас повторяюсь, но вследствии чего напряжение выростает в несколько раз? Вследствии изменения магнитного потока в катушке. Верно?

Нет, неверно. Напряжение возрастает в несколько раз вследствие уравнений Максвелла

Вот как. А я предпологал, что поток изменяется сразу после отключения.
Тогда должно же что то происходить с полем, что вызывает рост напряжения? Есть ли этому объяснение, помимо уравнений Максвелла?

[realeugene]

jast321 в сообщении #1325474 писал(а):

Есть ли этому объяснение, помимо уравнений Максвелла?

Вам их мало?

[Cos(x-pi/2)]

jast321 в сообщении #1325453 писал(а):

Ну так в первый момент времени для поддержания такого же тока оно должно быть ровно а два раза больше (если резисторы одинаковы) и тогда на каждом из резисторов будет такое же напряжение, как до отключения.

Это верно.

Заметьте ещё вот что:

До отключения батарейки напряжение на резисторах создавала батарейка. При этом напряжение на выводах катушки было равно нулю (если до отключения батарейки ток в катушку тёк практически постоянный). По теории, напряжение на выводах катушки равно $\frac{d \Phi}{dt}$ - это скорость изменения магнитного потока $\Phi.$ То есть ток тёк постоянный, магнитный поток в катушке был не равный нулю и постоянный, его скорость изменения была равна нулю. Всё в порядке, всё понятно.

В момент сразу же после отключения батарейки ток в катушке всё ещё прежний, магнитный поток $\Phi$ всё ещё прежний, но их скорость изменения скачком стала отличной от нуля. Эта ненулевая скорость изменения магнитного потока, т.е. величина $\frac{d \Phi}{dt}=L\frac{dI}{dt}\neq 0 $ и равна теперь суммарному напряжению на резисторах при всё ещё прежнем (в момент сразу же после отключения батарейки) токе и прежнем магнитном потоке $\Phi=LI.$

Чем больше сопротивление резисторов, тем больше при том же токе $I$ в катушке напряжение $\frac{d \Phi}{dt}=(R_1+R_2)I$ на её выводах. Это связано с тем, что чем больше сопротивление резисторов, тем больше при том же токе потребляемая резисторами от катушки мощность (больше скорость выделения тепла в резисторах $P=(R_1+R_2)I^2)$, и, значит, тем больше скорость ухода энергии из катушки. Т.е. при большом суммарном сопротивлении резисторов ток (и с ним магнитный поток) убывают быстрее, чем при маленьком сопротивлении резисторов. Всё в порядке, всё понятно.

Наверное, Вы в своих словесных рассуждениях путаете магнитный поток $\Phi$ и скорость его изменения $\frac{d \Phi}{dt}.$