Существует формула свертки, тогда

.
Что-то тут не так. Запишите формулу свертки для начала и найдите плотность суммы

. Процесс вычисления несколько трудоемок, потому что потребуется рассмотреть несколько случаев для переменной

. Когда вычислите плотность, интегрируйте ее, чтобы найти функцию распределения.
А вообще решение этой задачи гораздо удобнее получать из других соображений. Случайный вектор
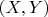
имеет равномерное распределение на квадрате
![$[0,2]^2$ $[0,2]^2$](https://dxdy-01.korotkov.co.uk/f/c/e/a/ceab3c3b6abe202ec09bca9ab28f213d82.png)
. Подумайте, что такое функция распределения суммы

в геометрических терминах. Как поймете, вы сможете сразу выписать

, без вычисления плотности.