Для изучения функции (2) рассмотрим ПРИЛОЖЕНИЕ I доказательства теоремы Ферма
ПРИЛОЖЕНИЕ I
В уравнении (7) можно в явном виде исключить переменную

и получить функцию переменной

при фиксированных натуральных

и

.Тогда получим уравнение (8)

.
Уравнение (8), так же как и уравнение (7), является необходимым условием существования экстремума функции (2) в произвольной точке с целыми координатами

и

.
Уравнение (8) так же можно рассматривать и как функцию

при фиксированных натуральных

и

.
Функция (8)

в ближайшей окрестности от точки

непрерывная, а в точке

функции (8) не определена, но можно вычислить предел, к которому стремится
функция (8) при


, для чего надо раскрыть неопределенность по правилу Лопиталя.
Раскроем неопределенность

Теперь найдем предел функции

при стремлении



.
Зависимость

показана на Рис. 1.

Теперь докажем, в точках ближайшей окрестности от точки

функция (8) имеет минимумы.
Рассмотрим произвольную точку с координатами

и

.
Теперь зададимся произвольным значением

и запишем функцию (2)

где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
.
Функцию (2) можно записать и в таком виде

где

при фиксированных

,

и

, то есть не зависят от


Функция

- синусоида, которая будет иметь минимум при

,
которое зависит от заданного значения

, то есть мы получаем зависимость

.
При изменении

изменяется и

, в которой функция будет иметь минимум.
То есть доказали, что каждому

соответствует свое

и свой минимум функции (2),
остается открытым только вопрос чему равен минимум функции (2), то есть равен минимум функции (2)
нулю или нет. То есть доказали, что в окрестности точки

функция (2) имеет минимумы,
координаты которого

при заданных

и
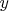
зависят от

.
На Рис.2 показано как перемещаются минимумы функции (2) в пространстве при изменении

.

Если приравнять функцию (2) нулю, то получим уравнение (9)

где
![$ z = \sqrt[n]{x^n+y^n} $ $ z = \sqrt[n]{x^n+y^n} $](https://dxdy-02.korotkov.co.uk/f/1/4/5/1456a7f75666ee992b993fefa8f3389782.png)
.
корнями уравнения (9) могут быть только целые числа,
то есть корнями уравнения (9) могут быть только корни уравнения Ферма.
Выводы:
1. Предел функции (8)

независимо от значений

и

равен 2, то есть

.
2. Переменная

и

, но рассматривать можно только целые значения

3. При значениях нецелых

функция (2) больше 0.
4. Чтобы функция (8)

была непрерывной, ее необходимо доопределить значением

.
5. Только значение корня

уравнения Ферма равно пределу функции (8)

,
другие корни уравнения Ферма, если они существуют, не равны пределу функции (8)

.