У нас ещё разнобой в обозначении радиальной координаты. Пусть будет

(хотя я сам больше люблю

). Итак, внутри и снаружи цилиндра, но не на поверхности

Договоримся скачок любой физической величины

на поверхности цилиндра обозначать
![$[u]$ $[u]$](https://dxdy-02.korotkov.co.uk/f/1/8/e/18e478f90f6a8448b1081c84c59af11b82.png)
и понимать это как разность предельных значений снаружи и изнутри (не наоборот).
Вы считаете, что
![$[E_n]=4\pi\sigma, [\frac{\partial\varphi}{\partial r}]=0$ $[E_n]=4\pi\sigma, [\frac{\partial\varphi}{\partial r}]=0$](https://dxdy-01.korotkov.co.uk/f/c/b/7/cb7ffa172d6aeb07793576da9151277582.png)
. С первым я согласен, но второе противоречит первому. Внешняя нормаль

к поверхности совпадает с базисным вектором
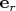
, так что

(в смысле внешнего или внутреннего предельного значения).