Песня "Где же нули у функции дзета?"(на мотив Sweet Betsy from Pike)
Где же нули у функции дзета?
Нам Риман оставил догадку про это:
«На критической линии, там они все,
А их плотность — один-на-два-
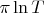
».
И эта гипотеза, словно заноза,
Многих людей довела до психоза.
Стремились они дать строгий расчет,
Что происходит, когда

растет.
Ландау, и Бор, и Крамер, и Харди
Среди одержимых шли в авангарде.
Но все-таки даже они не смогли
Уверенно все перечислить нули.
Впоследствии Харди сумел доказать,
Что на этой прямой их несметная рать,
Но его теорема все ж не исключает,
Что где-то еще те нули обитают.
Пусть

будет

минус
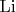
— вот прелестно!
Но как там с порядком

— неизвестно.
Если корень из
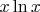
— потолок,
То Гипотезу Римана вывесть я б смог.
Вопрос про
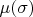
задал Линделёф;
Над ним потрудилось немало умов.
Проверим критическую полосу,
И сколько нулей там — как на носу.
Но функция эта ведет себя сложно,
Ее изучили, насколько возможно.
«График должен быть выпуклым, — смог он сказать, —
Если сигма сама превосходит 0,5».
Так где же нули у функции дзета?
Даже через столетие все нет ответа.
А ТРПЧ можно все улучшать,
Но контур обязан нулей избегать.
Тем временем Вейль обратился к предмету,
Используя более хитрую дзету.
Коль характеристика поля равна
Простому числу — теорема верна.
Мораль этой притчи нетрудно понять,
И всем юным гениям следует знать:
Если не выручает обычный подход,
То по модулю

— авось повезет!
Том М. Апостол, перевод Сергея Ельницкого
(Оригинал)
Where are the zeros of zeta of s?Where are the zeros of zeta of s?
G.F.B. Riemann has made a good guess:
«They're all on the critical line,» stated he,
«And their density's one over two
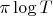
».
This statement of Riemann's has been like a trigger,
And many good men, with vim and with vigor,
Have attempted to find, with mathematical rigor,
What happens to

as
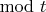
gets bigger.
The efforts of Landau and Bohr and Cramer,
Hardy and Littlewood and Titchmarsh are there.
In spite of their effort and skill and finesse,
In locating the zeros there's been no success.
In 1914 G.H. Hardy did find,
An infinite number that lie on the line.
His theorem, however, won't rule out the case,
That there might be a zero at some other place.
Let P be the function

minus
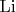
;
The order of

is not known for

high.
If square root of

times
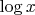
we could show,
Then Riemann's conjecture would surely be so.
Related to this is another enigma,
Concerning the Lindelöf function mu sigma,
Which measures the growth in the critical strip;
On the number of zeros it gives us a grip.
But nobody knows how this function behaves,
Convexity tells us it can have no waves.
Lindelöf said that the shape of its graph
Is constant when sigma is more than one-half.
Oh, where are the zeros of

of

?
We must know exactly. It won't do to guess.
In order to strengthen the prime number theorem,
The integral's contour must never go near 'em.
André Weil has improved on old Riemann's fine guess
By using a fancier

of

.
He proves that the zeros are where they should be,
Provided the characteristic is

.
There's a moral to draw from this long tale of woe
That every young genius among you must know:
If you tackle a problem and seem to get stuck,
Just take it mod p and you'll have better luck.