Решение Шварцшильда в другой инерциальной системе координат

[fizeg]

Как вы определяете декартовы координаты в данном случае и в чем видите ошибку?

[evgeniy]

А как Вы определяете криволинейные координаты? Если есть криволинейные координаты, то можно определить и декартовы координаты. Я не вижу ошибки, я задаю вопрос, в чем ошибка.

[fizeg]

evgeniy
Я их не определяю, я пытаюсь вас расшифровать

[schekn]

evgeniy в сообщении #1119722 писал(а):

Получится не диагональный метрический тензор, зависящий от декартовых координат

То, что Вы называете декартовыми координатами для Шварцшильда обычно называют "прямоугольными".
А ошибка у вас в том, что для метрики Шварцшильда тензор кривизны 4 ранга Римана-Кристоффеля отличен от нуля, а для плоского пространства-времени он всегда равен нулю.

[evgeniy]

По моему все и и так ясно. По метрическому тензору в криволинейной системе координат определен метрический тензор в декартовой системе координат. Первый метрический тензор определен из ОТО и измерен для проверки по траектории пробных частиц. Второй метрический тензор получается в результате вычислений. Зачем нужен второй метрический тензор? Для получения метрического тензора в двигающейся системе координат для одиночного тела. Для множества тел не получится, так как в случае множества тел система координат не инерциальная, одно тело действует на другое и есть внешнее воздействие на каждое тело. Для одного тела система координат инерциальная, так как на это одно тело не действуют внешние силы. Пробное тело не оказывает воздействие на массивное одиночное тело.

-- Вс май 01, 2016 10:42:56 --

schekn в сообщении #1119740 писал(а):

evgeniy в сообщении #1119722 писал(а):

Получится не диагональный метрический тензор, зависящий от декартовых координат

То, что Вы называете декартовыми координатами для Шварцшильда обычно называют "прямоугольными".
А ошибка у вас в том, что для метрики Шварцшильда тензор кривизны 4 ранга Римана-Кристоффеля отличен от нуля, а для плоского пространства-времени он всегда равен нулю.

При переходе от сферической системы координат к декартовой в случае метрики Шварцшильда не получится плоское пространство, и тензор кривизны не будет равен нулю в декартовых координатах. В случае метрики Шварцшильда тензор $g_{00},g_{rr}$ не совпадает с метрическим тензором сферической системы координат. Точно также при записи решения Шварцшильда в декартовой системе координат не получится единица,. не получится диагональный тензор, а будет тензор общего вида. Попробуйте произвести вычисления.

[Munin]

evgeniy в сообщении #1119722 писал(а):

Переходим в декартову систему координат по формулам

Очень жаль, но нет, не переходите.

-- 01.05.2016 10:16:25 --

evgeniy в сообщении #1119736 писал(а):

Если есть криволинейные координаты, то можно определить и декартовы координаты.

Это только в плоском пространстве.

Если у вас есть лист бумаги, то на нём можно нарисовать и прямоугольную сетку координат, и криволинейную. Если у вас есть мяч, то криволинейную сетку координат на нём нарисовать можно, а прямоугольную - нельзя. Любая будет криволинейной.

Да, я помню, что в ЛЛ-2 это довольно плохо было акцентировано. Стоит почитать МТУ, Вайнберга, или учебники по дифференциальной геометрии.

[evgeniy]

Munin в сообщении #1119750 писал(а):

evgeniy в сообщении #1119722 писал(а):

Переходим в декартову систему координат по формулам

Очень жаль, но нет, не переходите.

Я могу выписать формулы, по которым осуществляется переход
$ds^2=g_{00}dt^2-g_{rr}dr^2-r^2(d\theta^2+\sin^2 \theta d\varphi^2)=$
$=g_{00}dt^2 +\sum_{l=1}^3 g_{ll}(dq^l)^2=g_{00}dt^2 +\sum_{l=1}^3 g_{ll}\frac{\partial q^l}{\partial x^p}\frac{\partial q^l}{\partial x^q}dx^pdx^q$=
$=g_{00}dt^2 +h_{pq}dx^pdx^q;h_{pq}=\sum_{l=1}^3 g_{ll}\frac{\partial q^l}{\partial x^p}\frac{\partial q^l}{\partial x^q}$
$h_{pq}\ne-\delta_{pq}$
Что в этих формулах не правильно?

[schekn]

evgeniy в сообщении #1119744 писал(а):

Попробуйте произвести вычисления.

Непонятно в чем у вас проблема. В "прямоугольных" координатах метрику Шварцшильда можно посмотреть у Вайнберга или в учебнике Брумберга. Затем подставляете преобразования Лоренца.

[evgeniy]

schekn в сообщении #1119754 писал(а):

evgeniy в сообщении #1119744 писал(а):

Попробуйте произвести вычисления.

Непонятно в чем у вас проблема. В "прямоугольных" координатах метрику Шварцшильда можно посмотреть у Вайнберга или в учебнике Брумберга. Затем подставляете преобразования Лоренца.

Если в учебниках есть метрика движущегося тела, то я очень рад. Скажете это
Munin, а то он пишет

Munin в сообщении #1119750 писал(а):

Очень жаль, но нет, не переходите.

[Munin]

evgeniy в сообщении #1119753 писал(а):

Что в этих формулах не правильно?

То, что это не декартова система координат.

[schekn]

evgeniy в сообщении #1119756 писал(а):

Если в учебниках есть метрика движущегося тела, то я очень рад.

Метрики движущегося тела там нет. Как раз вы хотите ее нам предоставить, насколько я понял.

[evgeniy]

Munin в сообщении #1119750 писал(а):

evgeniy в сообщении #1119722 писал(а):

Переходим в декартову систему координат по формулам

Очень жаль, но нет, не переходите.

-- 01.05.2016 10:16:25 --

evgeniy в сообщении #1119736 писал(а):

Если есть криволинейные координаты, то можно определить и декартовы координаты.

Это только в плоском пространстве.

Если у вас есть лист бумаги, то на нём можно нарисовать и прямоугольную сетку координат, и криволинейную. Если у вас есть мяч, то криволинейную сетку координат на нём нарисовать можно, а прямоугольную - нельзя. Любая будет криволинейной.

Да, я помню, что в ЛЛ-2 это довольно плохо было акцентировано. Стоит почитать МТУ, Вайнберга, или учебники по дифференциальной геометрии.

Да Вы правы, мне и Shwedka об этом говорила. Нельзя на поверхности трехмерного тела построить два ортогональные угла. Значит в не плоском пространстве не все системы координат реализуются. Интересно, какие еще системы координат не реализуются в не плоском пространстве.

Но как я понимаю для одиночного тела пространство плоское, так как оно инерциальное, и для него можно построить декартову систему координат. Для нескольких тел нельзя построить декартову систему координат.

[Munin]

evgeniy в сообщении #1119763 писал(а):

Значит в не плоском пространстве не все системы координат реализуются.

И в плоском аналогично. Например, на плоскости нельзя построить стандартную для сферы систему координат широты и долготы.

evgeniy в сообщении #1119763 писал(а):

Интересно, какие еще системы координат не реализуются в не плоском пространстве.

Их бесконечно много.

По сути, никакие системы координат, которые существуют в плоском пространстве, невозможны в неплоском пространстве. И дальше, для каждого неплоского пространства свои классы систем координат разные.

evgeniy в сообщении #1119763 писал(а):

Но как я понимаю для одиночного тела пространство плоское

Если оно достаточно массивно, чтобы создавать гравитационное поле, - то нет, неплоское. Его гравитационное поле - шварцшильдово, то самое, которое вы упоминали в самом начале темы.

[evgeniy]

Munin в сообщении #1119774 писал(а):

По сути, никакие системы координат, которые существуют в плоском пространстве, невозможны в неплоском пространстве. И дальше, для каждого неплоского пространства свои классы систем координат разные.

evgeniy в сообщении #1119763 писал(а):

Но как я понимаю для одиночного тела пространство плоское

Если оно достаточно массивно, чтобы создавать гравитационное поле, - то нет, неплоское. Его гравитационное поле - шварцшильдово, то самое, которое вы упоминали в самом начале темы.

НЕ совсем понял. Например сферическая система $r,\theta,\varphi$ координат плоская, ее можно пересчитать в декартову, она существует как плоскость в четырехмерном пространстве, а реализуется в не плоском пространстве ОТО, пространственная часть которого находится на поверхности четырехмерного не плоского тела. Тут какое-то не понимание. Впрочем этот вопрос требует точной терминологии и его можно опустить, иначе завязнем.

Также я не понял на счет массивного одиночного тела. На него не действуют внешние силы, значит оно находится в инерциальной системе отсчета параграф 1 ЛЛ2 и для него справедливо преобразование Лоренца. Раз тело находится в инерциальной системе координат, значит пространство для него плоское параграф 82 ЛЛ2. Если следовать этим параграфам то противоречия у ЛЛ нет. Для пробного заряда пространство искривленное. Пример Солнце, пространство для него плоское и оно движется с постоянной скоростью в инерциальной системе отсчета. Оно создает не плоское пространство, но само находится в плоском пространстве. Планеты Солнечной системы находятся в гравитационном поле Солнца и пространство для них не плоское. Двойные звезды, обе большой массы воздействуют друг на друга и каждое находится в не плоском пространстве. Планеты не воздействуют на Солнце, и поэтому пространство для него плоское.

[Munin]

evgeniy в сообщении #1119787 писал(а):

НЕ совсем понял. Например сферическая система $r,\theta,\varphi$ координат плоская, ее можно пересчитать в декартову, она существует как плоскость в четырехмерном пространстве

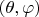
Верно. Но система координат $(\theta,\varphi)$ на сфере - не плоская, и её нельзя пересчитать в декартову $(x,y)$ - потому что на сфере декартову систему координат нанести нельзя.

evgeniy в сообщении #1119787 писал(а):

Например сферическая система $r,\theta,\varphi$ координат... реализуется в не плоском пространстве ОТО, пространственная часть которого находится на поверхности четырехмерного не плоского тела.

Это у вас заблуждение и недопонимание.

И нет, это нельзя "опустить", это ключевой момент. ОТО - это теория искривлённого пространства-времени. Если вы не понимаете, что такое искривлённое пространство, и чем отличается от плоского, то вы в ОТО не понимаете ни-че-го. Так что, это первый пункт.

evgeniy в сообщении #1119787 писал(а):

Также я не понял на счет массивного одиночного тела.

Оно создаёт гравитационное поле. Гравитационное поле измеряется пробными телами. А пробное тело - это уже второе тело.

evgeniy в сообщении #1119787 писал(а):

значит оно находится в инерциальной системе отсчета параграф 1 ЛЛ2 и для него справедливо преобразование Лоренца.

Этот параграф теряет свою применимость, при учёте гравитации и при наличии гравитационного поля. Это чётко сказано в § 82.

evgeniy в сообщении #1119787 писал(а):

Раз тело находится в инерциальной системе координат, значит пространство для него плоское параграф 82 ЛЛ2. Для пробного заряда пространство искривленное.

Нету никаких "для". Есть единое пространство-время, в котором находятся все тела. Оно искривлено. За счёт первого - массивного - тела. Второе - пробное - тело имеет настолько малую массу, что существенных искривлений не производит. Оно используется для того, чтобы обнаружить искривление пространства-времени, созданное первым телом.

Вот этот вот факт, что пространство-время для всех едино, - не очень чётко произнесён в ЛЛ-2. Это недостаток изложения этого учебника. В других учебниках можно это прочитать более явно.