Для этого функция

должна удовлетворять очевидным условиям, а именно:
1)

;
2)для любого


;
3)для любых неотрицательных

если
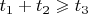
, то

.
Попытался доказать пункт 3 для произвольной выпуклой функции, т.е. такой функции, что

для любых
![$p \in [0, 1]$ $p \in [0, 1]$](https://dxdy-02.korotkov.co.uk/f/5/0/8/50859084573563ccfeaa033e73d1b04482.png)
.
Не смог. Подскажите идею, что ли.
При

легко получаем уже цитированное неравенство

. Ну и дальше что? Если бы из выпуклости функции удалось доказать, что для любых неотрицательных

верно

, тогда все было бы просто: берем выпуклую возрастающую функцию и получаем, что для любых неотрицательных

если
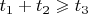
, то

. Ну и как это доказать? Это вообще верно?