Об учебнике Мордковича

[Nemiroff]

Kras в сообщении #989308 писал(а):

Вернее не осилил, там уныние настоящее.

Мда. Две точки --- противоположные вершины прямоугольника. на границе этого прямоугольника в уме находим точку, до которой расстояния одинаковы (точнее две точки). Две точки дают отрезок. Если из такой точки сместиться по координатной оси не вдоль стороны прямоугольника, расстояние не изменится. А дальше очевидно, что добавятся лучи --- два, если наши точки не в вершинах, и сразу целые углы, если в вершинах.
В числах даже считать неохота --- получается загогулина, иногда вырождающаяся либо в евклидов случай, либо в два угла с перемычкой.

[Munin]

Nemiroff
Я щас пожалуюсь модераторам на приведение решения простой учебной задачи :-)

[Nemiroff]

Ну да.
С другой стороны, ТС все равно решать ничего не хочет, а я даже чисел не писал.

[Kras]

Nemiroff в сообщении #989367 писал(а):

на границе этого прямоугольника в уме находим точку, до которой расстояния одинаковы (точнее две точки). Две точки дают отрезок.

Я понял, вы взяли стороны параллельные координатным осям (для любого другого прямоугольника такие рассуждения не подойдут). Задача в целом непростая, но, как мне кажется, довольно бесполезная.

Nemiroff в сообщении #989367 писал(а):

евклидов случай

Что такое евклидов случай?

Nemiroff в сообщении #989367 писал(а):

два угла с перемычкой

Перемычка - это отрезок? Отрезок не обязан соединять вершины углов.

Munin в сообщении #989362 писал(а):

Я хотел показать, что предложенное вами определение прямой неудачно.

Проблемы возникают уже в пространстве.
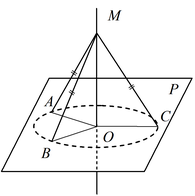
Геометрическим местом точек, равноудаленных от трех данных точек $A$, $B$ и $C$ пространства, не лежащих на одной прямой, является прямая $MO$.

В первом определении нам требовалось, чтобы две точки не совпадали. Теперь нужно, чтобы три точки не лежали на одной прямой. Рекурсия. Если ещё экспериментировать с понятием расстояния, то мы получим разные ситуации, может быть даже не имеющие сходства с прямой. То есть у меня получилось действительно неудачное определение.

[Munin]

Kras в сообщении #989761 писал(а):

Что такое евклидов случай?

То, что вы изучали в школе, называется евклидова геометрия. В частности, метрика в ней имеет вид $L^2.$

[Nemiroff]

Kras в сообщении #989761 писал(а):

Задача в целом непростая

Задача элементарная.

Kras в сообщении #989761 писал(а):

Перемычка - это отрезок?

Перемычка — это отрезок.

Kras в сообщении #989761 писал(а):

Отрезок не обязан соединять вершины углов.

Я не знаю, кто что обязан — в ответе будет соединять.

Как я и предполагал, признание ошибок в планы не входит.

[Kras]

Nemiroff
Да, всё же будет соединять...