в точной формуле потенциалов Лиенара-Вихерта (63,8) ЛЛ2, есть максимум вторая производная. Именно на эту нестыковку я и обратил внимание ув.Cos(x-pi/2).
vlapayНету нестыковки, и
svv уже пояснил почему нету. Формулы Лиенара-Вихерта для ЭМ-полей хотя и точные, но в них входит координата, скорость и ускорение заряда, взятые в неизвестный нам момент времени

который определяется неявно уравнением

В системе нескольких частиц у каждой частицы вектор

свой, и поэтому момент времени

- свой, индивидуальный. Поэтому надо ещё сильно попотеть, чтобы реально вычислить поля по формуле Лиенара-Вихерта
точно. Чтобы получить считабельный ответ, нужны приближения.
Дык, как раз о приближениях у нас и была речь (правда, зря я занялся "подогонкой ответа" под фейнмановский способ построения поля ЭМ-излучения, раз этот способ Вам оказался неизвестен; на самом-то деле обоснованный способ вычисления другой - через запаздывающий векторный потенциал, как в ЛЛ-2, но ответ для напряжённостей полей в итоге получается такой же). Приближения такие: 1) характерный размер

системы зарядов считается малым по сравнению с расстоянием

от неё до точки наблюдения поля; 2) этот размер

мал также по сравнению с длиной волны

где

- характерная частота движения зарядов в системе.
Вот в таких приближениях и получаются формулы полей


с производной от ускорения зарядов, т.е. с третьей производной от координат частиц. Кстати, в вашей оценке запаздывания для квадрупольного вибратора у Вас тоже ж появилась производная от ускорения - и Вы не назвали это "нестыковкой". И Ландау-Лифшиц (взяв с Вас пример ;) смело написали третью производную от координат: посмотрите их формулы поля (71.4) в

"Квадрупольное и магнитно-дипольное излучения" (у нас такие же формулы получились).
Понимать это можно так. Если движение зарядов характеризуется частотой
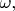
то каждая очередная производная по времени даёт в амплитуду поля множитель

Заметьте, что в наших приближениях появилось и произведение координат, т.е. увеличилась степень характерной амплитуды колебаний координат

: в дипольном приближении поле было пропорционально

а в квадрупольном оно пропорционально

Значит, можно считать, что приближения основаны на разложении поля по степеням малого параметра

(и об этом чётко говорится в самом начале

ЛЛ-2).
В свою очередь это означает, что пользоваться этими приближёнными формулами можно только в достаточно "низкочастотных" примерах. Движение зарядов не обязательно должно быть гармоническим колебанием; оно может иметь фурье-составляющие с разными частотами, но и для наибольшей частоты требуется выполнение условия

Примеры же со скачкообразным изменением ускорения не выявляют "нестыковки", а просто выходят за рамки применимости наших формул: скачкообразному изменению соответствует широкий фурье-спектр частот, включающий с немалыми амплитудами очень высокие частоты. Если умеете считать такие примеры по точной формуле Лиенара-Вихерта, то, как говорится, флаг Вам в руки...
Так... Про спин гравитона. Вроде, выше всё уже обсудили; и не один раз. Если Вы как-то по своему определяете понятие "спин", да ещё и не верите в ОТО, то это факт вашей биографии, больше никак не могу прокомментировать...
На самом деле это всё не аргумент. Если у нас есть только электрические заряды с одинаковым соотношением заряд/масса (как в гравитации), то мы получим точно такую же картину. Но, из наших трудностей, в этом случае, с регистрацией электромагнитных волн, ещё не следует что векторных электромагнитных волн не существует.
Дык вся суть-то в том, что в природе
есть заряды
с разным соотношением заряд/масса; в частности, есть электронейтральные тела и есть частицы заряженные с разным знаком; поэтому мы реально
можем, если захотим, обнаруживать векторные ЭМ-волны. А вот тел, нейтральных к гравитации (или с массами разного знака), -
нет в природе, хоть убейся! Поэтому при всём желании Вы не можете обнаружить гравитационый аналог векторной ЭМ-волны: можете хоть тыщу раз повторить слова "она существует", но обнаружить-то не можете в опытах ни с какими частицами, а это с точки зрения физики то же самое, что "не существует".
Собс-но, это ключевой момент в ОТО: да, можно описывать гравитацию как поле в плоском пространстве-времени Минковского, без "заморочек с кривизной", но в итоге оказывается, что у нас нет приборов, с помощью которых можно было бы проверить на опыте такое описание. Гравитация действует поголовно на все объекты и приборы, и как раз так, как если бы ПВ-было искривлённым, а "фоновое" плоское ПВ Минковского в такой теории оказывается ненаблюдаемым. Собс-но, об этом в учебниках как раз и написано.



