Спин гравитона равен единице?

[vlapay]

Посмотрим на излучение гравитационных волн с новой точки зрения.
Формула (13) из статьи в физической энциклопедии (она же ф.110,16 ЛЛ2) удивительно похожа на формулу (71.5 ЛЛ2) без первого и третьего члена, которая описывает квадрупольное излучение системы частиц с одинаковым соотношением заряд/масса. Излучение рождает силу радиационного торможения, которая так же описывается аналогично для случая малых скоростей движения масс и зарядов и зона движения намного меньше длины излучаемой волны. Сила радиационного торможения не только уменьшает энергию систему движущихся зарядов, но и изменяет её момент импульса. Несмотря на то, что гравитационное излучение в четыре раза сильнее аналогичного квадрупольного электромагнитного излучения, на единицу излучённой энергии приходится одинаковое изменение момента импульса системы, хотя спин гравитона, по ОТО, в два раза больше спина фотона. В рамках ОТО эта разница объясняется тем, что угловое распределение излучения гравитонов и фотонов разное.
Но есть определённые сомнения в том, что это так в реальности, тем более, что нет экспериментальных данных по угловому распределению гравитационного излучения. Предположим, что у нас есть поляризованная гравитационная волна с максимальным значением спина гравитонов - каждый поглощённый гравитон изменяет момент импульса системы, в которой он поглотился, на $2\hbar$. Гравитационная волна, так же, как и электромагнитная, воздействует на систему движущихся "зарядов", изменяя их скорость, импульс и момент импульса. Чтобы момент импульса, который передаст волна движущемуся заряду, был максимальным на единицу энергии, надо, чтобы заряд двигался по окружности. Энергия, которая передаётся заряду, равна $E=FVt=F\omega Rt$, момент импульса $M=FRt$, отсюда $E=M\omega$. На один квант излучения $E=\hbar\omega$ приходится момент импульса $M=1\hbar$. Это максимальный момент импульса на один квант излучения и он равен единице. Сам волновой пакет может переносить и больший момент импульса, но это за счёт импульсов квантов излучения, а не спина самого кванта (орбитальный момент). Мы же рассматриваем одночастичное поглощение с максимально возможным переносом момента импульса, когда размер поглощающей системы гораздо меньше длины волны.
Не хочу фантазировать на тему, почему спин гравитона должен быть именно единице, а не двум, так как нет альтернативной ОТО теории с таким спином гравитона. Отмечу только, что из равенства спинов гравитона и фотона ещё не следует их идентичность, так как гравитон, в отличии от фотона, содержит и тензорную компоненту, поэтому мощность излучения гравитационных волн выше, чем у электромагнитного аналога.

[Munin]

Спин 2 следует из того что массы одинакового знака не отталкиваются, а притягиваются. Спин 1 дал бы отталкивание.

Спин 2 экспериментально подтверждён в 1919 году в наблюдениях отклонения света Солнцем: знаменитая "цифра в 2 раза больше, чем по теории Ньютона".

Разумеется, какие-то другие формулы теорий спина 1 и спина 2 похожи. Но не эти формулы служат аргументами за то, что спин гравитона 2. И разумеется, альтернативные теории спина 0 и 1 были построены давным-давно, просто чтобы сравнить предсказания, и по всем наблюдениям выбор делается именно в пользу спина 2. (Можно усложнить теорию, допустив смешивание спинов 0 и 2 (скалярно-тензорная теория), или даже 0, 2 и 4, но надобности в этом никакой нет.) Написано об этом, например, в МТУ.

[vlapay]

Munin в сообщении #976851 писал(а):

Спин 2 следует из того что массы одинакового знака не отталкиваются, а притягиваются. Спин 1 дал бы отталкивание.

Вы привели свой аргумент, я привёл свой. Разобраться в моих аргументах несложно, и найти ошибку, если она есть. Вы это можете сделать? По вашему аргументы ничего по сути сказать не могу, так как не владею этой информацией. Если вы ничего не возразите на мой аргумент, то сохранится статус кво.

Цитата:

Спин 2 экспериментально подтверждён в 1919 году в наблюдениях отклонения света Солнцем: знаменитая "цифра в 2 раза больше, чем по теории Ньютона".

Ну это вы сказанули... Пока даже гравитационные волны не зарегистрированы на Земле, а у вас уже даже спин гравитона измерен. Двойное отклонение света несколько из другой оперы.

Цитата:

Разумеется, какие-то другие формулы теорий спина 1 и спина 2 похожи. Но не эти формулы служат аргументами за то, что спин гравитона 2. И разумеется, альтернативные теории спина 0 и 1 были построены давным-давно, просто чтобы сравнить предсказания, и по всем наблюдениям выбор делается именно в пользу спина 2. (Можно усложнить теорию, допустив смешивание спинов 0 и 2 (скалярно-тензорная теория), или даже 0, 2 и 4, но надобности в этом никакой нет.) Написано об этом, например, в МТУ.

Представьте на секунду, что в нашем мире есть только электрические заряды с одинаковым соотношением заряд/масса. Система из таких зарядов не может регистрировать плоские э-м волны, так как ускорение всех элементов будет одинаковым. Точнее, будут слабые релятивистские эффекты (парадокс Белла), но амплитуда отклонений геодезических будет пропорциональна квадрату амплитуды э-м волны. Других зарядов у нас, а те, что есть, плоские э-м волны не может регистрировать. Но ведь это не означает, что таких волн нет в природе.
Надо внимательно смотреть на основы теории. Если мы постулируем принцип эквивалентности инерционной и гравитационной массы (одинаковое для всех соотношение заряд/масса) и измерение только относительных смещений реперов, то мы попадаем в вышеописанную ловушку не совсем адекватного описания физических явлений. Получается, что наши возможности измерений слишком убоги, чтобы получить правильные результаты.

В стартовом посте я привел простой и понятный аргумент, почему спин гравитона равен единице. Прошу, в первую очередь, высказываться именно по этому аргументу.

[Pphantom]

Прошу:
1) Munin - привести более конкретные ссылки на источники (насколько я могу судить, это несложно), дабы vlapay овладел информацией.
2) vlapay - уменьшить степень категоричности высказываний и, после выполнения п.1, указать конкретные ошибки в приведенных источниках, позволяющие дезавуировать полученные там результаты.

[vlapay]

Pphantom в сообщении #976880 писал(а):

2) vlapay - уменьшить степень категоричности высказываний и, после выполнения п.1, указать конкретные ошибки в приведенных источниках, позволяющие дезавуировать полученные там результаты.[/mod]

Это как понимать - я должен искать ошибки в приведённых мне аргументах, а в моих аргументах искать ошибки не нужно? Интересный подход. Спрашивается - зачем было открывать тему, если никто не может или не хочет в ней разбираться? Мне, в первую очередь интересно, где у меня ошибка, а не у коллективного разума.

[Munin]

Несложно, но позже вечером.

[Pphantom]

vlapay в сообщении #976886 писал(а):

Это как понимать - я должен искать ошибки в приведённых мне аргументах, а в моих аргументах искать ошибки не нужно? Интересный подход.

Ну что ж, объясню. Это "Дискуссионные темы", а не "Помогите решить, разобраться".

Во ПРР будут искать Ваши ошибки, но там Вы будете читать то, что Вам пишут, а не "приводить аргументы" и требовать их от окружающих. В этом разделе обоснование того, почему Ваши результаты не совпадают с ранее полученными - Ваша задача.

Munin в сообщении #976887 писал(а):

Несложно, но позже вечером.

Хорошо, ждем.

[Ms-dos4]

Да какие тут ссылки то могут быть. Любой более-менее современный учебник по гравитации. Можно например Фейнмановские лекции по гравитации посмотреть, лекция №3.

[vlapay]

Ms-dos4 в сообщении #976899 писал(а):

Да какие тут ссылки то могут быть. Любой более-менее современный учебник по гравитации. Можно например Фейнмановские лекции по гравитации посмотреть, лекция №3.

Хорошо, посмотри на этот учебник. В лекции №3 написано, что, при наличии ненулевой массы, возможны все проекции спина. Например, в теории Логунова постулируется ненулевая масса гравитона, с чем я полностью согласен, поэтому возможны все проекции спина 2. У Фейнмана спин 0 был искусственным образом исключён из окончательного решения. Я не утверждаю, что возможно исключить, подобным образом, спин 2 из теории с массивным гравитоном, но это желательно, потому что в стартовом посте доказано, что реально квант излучения может переносить не более 1 единицы постоянной Планка. Такой ответ Вас устроит?

[Ms-dos4]

vlapay
Ненулевая масса гравитона вообще приводит к огромным проблемам (и кстати, я не помню, что бы в лекции №3 у него обсуждалась гравитация с массивным гравитоном, так что откуда вы взяли заключения о ненулевой массе мне неизвестно, хотя возможно я и запамятовал), поэтому рассматривать её в общем то особого смысла нет. А у вас в посте я вообще никаких доказательств не вижу. Какая то каша бессмысленная написана.

[vlapay]

Ms-dos4 в сообщении #976938 писал(а):

vlapay
Ненулевая масса гравитона вообще приводит к огромным проблемам (и кстати, я не помню, что бы в лекции №3 у него обсуждалась гравитация с массивным гравитоном, так что откуда вы взяли заключения о ненулевой массе мне неизвестно, хотя возможно я и запамятовал), поэтому рассматривать её в общем то особого смысла нет.

Там пишется о доказательстве Вигнера, о том, что из нулевой массы гравитона или фотона следует всего две проекции спина.

Цитата:

А у вас в посте я вообще никаких доказательств не вижу. Какая то каша бессмысленная написана.

Так не интересно. Я не поленился и вашу ссылку прочитал, а вы пару моих абзацов не можете. Munin как-то смог разобраться, попробуйте ещё раз.

[Munin]

Мизнер, Торн, Уилер. Гравитация.
Том 1, глава 7, § 7.1. Там 12 страниц, но все они имеют отношение к заданному вопросу. Также of interest может быть глава 39. Но по главам 39, 40 может сложиться, что ОТО сегодня проверена только в ньютоновском и ППН-приближении - это не так. На момент написания книги, это было так, а с тех пор были открыты чёрные дыры и точно измерены космологические параметры - это всё выходит за рамки приближений слабого поля.

Фейнман, Мориниго, Вагнер. Фейнмановские лекции по гравитации.
Лекция 3, пункт 3.1 "Спин гравитона". Это не слишком часто обсуждаемый, но хорошо известный в теорфизике факт. Приведу для примера ещё ссылку: Пескин, Шрёдер. Введение в квантовую теорию поля. Глава 4, пункт 4.8.

-- 11.02.2015 23:57:22 --

vlapay в сообщении #976927 писал(а):

потому что в стартовом посте доказано, что реально квант излучения может переносить не более 1 единицы постоянной Планка.

К сожалению, ничего там не доказано, а высосана из пальца пара формул.

vlapay в сообщении #976927 писал(а):

Например, в теории Логунова постулируется ненулевая масса гравитона, с чем я полностью согласен, поэтому возможны все проекции спина 2.

Все проекции - это не то же самое, что все спины. Теория с массивным гравитоном - это не то же самое, что скалярно-тензорная теория.

vlapay в сообщении #976950 писал(а):

Там пишется о доказательстве Вигнера, о том, что из нулевой массы гравитона или фотона следует всего две проекции спина.

Ну и при чём оно здесь? Проекция спина и сам спин - вещи разные.

vlapay в сообщении #976950 писал(а):

Я не поленился и вашу ссылку прочитал

Ну, это ещё не значит, что понял...

[Pphantom]

Ну что ж, ссылки представлены, спасибо, искомые утверждения в них действительно содержатся. vlapay, увы, но Вам придется объяснять, почему Фейнман и МТУ ошиблись. Очень желательно при этом обращаться к собеседникам на "Вы".

[Cos(x-pi/2)]

Извините, с запозданием добавлю ответ на вопрос в теме.

vlapay в сообщении #976886 писал(а):

Спрашивается - зачем было открывать тему, если никто не может или не хочет в ней разбираться? Мне, в первую очередь интересно, где у меня ошибка, а не у коллективного разума.

vlapay
Ваш абзац про "удивительную похожесть" классических формул излучения оставлю без внимания, а в той части, где Вы строите свою аргументацию на утверждениях:

Цитата:

Энергия, которая передаётся заряду, равна $E=FVt=F\omega Rt$, момент импульса $M=FRt$, отсюда $E=M\omega$. На один квант излучения $E=\hbar\omega$ приходится момент импульса $M=1\hbar$

укажу ошибку.

Даже если мы закроем глаза на легковесность указанного аргумента (он ведь не тянет на доказательство) и продолжим рассуждать на этом языке, то прежде всего мы должны заметить следующее отличие ЭМ-волны от грав. волны.

Представим себе излучатель ЭМ-волны с круговой поляризацией, т.е. - излучатель волны с вращающимся электрическим полем $\mathbf{E}$, - как вращающийся диполь: два одинаковых тела с противоположными зарядами $q$ и $-q$, укреплённые на концах стержня, вращаются вокруг своего центра масс (вокруг оси, препендикулярной стержню) с частотой $\omega=2\pi /T,$ где $T$ - временной период возникающей при этом ЭМ-волны. Приёмник этого ЭМ-излучения можно представить себе таким же образом - как диполь, вращающийся под действием падающего на него вращающегося поля $\mathbf{E}$ с частотой $\omega.$ В своей аргументации Вы используете такую картину вращения заряженных тел, так как пользуетесь формулой для скорости $V=\omega R,$ то есть: $V=\omega R=2 \pi R/T,$ - в этой формуле подразумевается, что за период $T$ каждое пробное тело-заряд, над которым эл. поле волны совершает работу, проходит путь $2 \pi R,$ т.е. тело делает полный оборот.

Чтобы перенести эту аргументацию на грав. волну, мы должны рассмотреть аналогичный вращающийся излучатель. Грав. волна порождается массами, а массы не могут иметь противоположных знаков, поэтому излучателем грав. волны с круговой поляризацией пусть служат просто два одинаковых тела (с массами $m$ и $m$), укреплённые на концах стержня, вращающиеся вокруг своего центра масс. Так вот, заметим: один временной период $T$ грав. волны порождается одним полуоборотом этой пары масс (т.к. уже после полуоборота расположение обех масс неотличимо от начального, и, значит, следующим полуоборотом порождается снова такая же конфигурация волны, - соответствующая целому периоду). Соответственно, приёмником может служить аналогичная пара одинаковых масс, и она будет под действием этой грав. волны вести себя аналогично излучателю - будет делать половину оборота за время $T=2 \pi / \omega.$

Значит, теперь в Вашей формуле для работы $E=FVt$ скорость $V$ должна быть равна $ \pi R /T=\omega R/2.$ И тогда Ваша исправленная аргументация должна звучать так:

"Энергия, которая передаётся приёмнику грав. волны, равна $E=FVt=F (\omega /2) Rt$, момент импульса $M=FRt$, отсюда $E=M\omega /2$. На один квант излучения $E=\hbar\omega$ приходится момент импульса $M=2\hbar.

Добавлю ещё ссылку на гораздо более серьёзную аргументацию:

Мизнер, Торн, Уилер. Гравитация.
Том 3, глава 35 "Распространение гравитационных волн", § 35.6 "Поляризация плоской волны" стр. 172 - 176. Там Вы найдёте сравнение эл. волны с грав. волной, более подробное обсуждение картины движения пробных тел под действием волны (а на указанном Вами сайте она почти не пояснена), и, что особенно важно, - метод определения спина из трансформационных свойств поля при поворотах; процитирую (с пропусками):

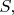
"Заметим из фиг. 35.2, что в любой момент времени гравитационная волна инвариантна относительно поворота на $180^{\circ}$ вокруг направления ее распространения. Аналогичный угол для электромагнитных волн (фиг. 35.1) составляет $360^{\circ},$ а для волн, связанных с нейтрино, этот угол равен $720^{\circ}.$" <...> Классическое поле излучения, соответствующее частице со спином $S,$ всегда инвариантно относительно поворота на угол $360^{\circ}/S$ вокруг направления распространения."

[Munin]

Cos(x-pi/2)
Ваши посты читать всегда приятно, а тут ещё спасибо за объяснения сути формул.