Моя тема курсовой - исследование функциональных полей. Мне предложили работать по книжке Henning Stichtenoth - Algebraic function fields, но уже из первого определения я понял, что без помощи я во всем этом не разберусь, хотя и смогу что-нибудь написать.
Само определение:
Definition 1.1.1. An algebraic function field

of one variable over

is an extension field

such that

is a finite algebraic extension of

for some element

which is transcendental over

.
Как я должен представлять себе это поле? Мне сказали, что оно строится в два этапа:
1) Первое расширение чисто трансцендентное, получается из

присоединением некоего трансцендентного над

элемента

;
2)второе расширение конечное алгебраическое, т.е. получается из поля

присоединением к

корня некоего неприводимого многочлена над этим полем.
И сразу вопросы:
1) Что значит "построить расширение поля присоединением к нему некоего элемента"? Просто взяли этот воображаемый элемент и закинули его в исходное множество, а потом сказали, что это такое расширение? Или в этом какой-то глубокий смысл?
2) Мы присоединяем трансцендентный над

элемент. То есть нет ни одного многочлена с коэффициентами из

, для которого этот элемент был бы корнем. Тогда откуда мы взяли этот элемент?
Вспомним, как мы строили конечные поля как расширение данного поля
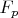
. У нас есть некоторый многочлен, неприводимый над
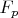
, и возводя в степени его корень, мы получаем
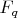
- расширение поля
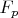
. Аналогичные утверждения: мы построили расширение поля, присоединив к нему корень неприводимого над
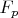
многочлена; мы факторизовали множество всех многочленов по данному неприводимому многочлену; расширение
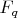
- это множество корней многочлена

над
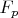
.
А чем отличается построение этих наших двух полей от такого построения поля?
3) Что значит запись

? Она чем-то отличается от обозначения множества всех многочленов
![$K[x]$ $K[x]$](https://dxdy-03.korotkov.co.uk/f/a/2/0/a20d83b3d0b996bc9ef02e0862d7b0b482.png)
от одной переменной

?
4) Как выглядят элементы поля алгебраических функций? Где-то я читал, что это поле состоит из дробей вида

, где

и

- многочлены, коэффициенты которых тоже являются многочленами.
Объясните максимально просто, как строится это поле и что оно вообще из себя представляет.



