Инвариантность размерности пространства

[_hum_]

В соседней ветке зашла речь про трехмерность нашего пространства. Обычно, в обывательском смысле, трехмерность - это необходимость указания трех чисел для задания любой точки пространства. Но три числа всегда можно закодировать одним. Насколько я понимаю, слабейшее (?) условие, которое запрещает это делать, это непрерывность (в обе стороны?) способа кодирования. Получается, что непрерывность каким-то фундаментальным образом оказывается связанной с геометрией нашего пространства. И интересно было бы узнать, что это за связь. (Где в доказательстве соответствующего факта и в какой форме всплывает непрерывность?)

[Munin]

_hum_ в сообщении #907169 писал(а):

Получается, что непрерывность каким-то фундаментальным образом оказывается связанной с геометрией нашего пространства. И интересно было бы узнать, что это за связь.

Эту связь изучает наука топология. Почитайте.

[Oleg Zubelevich]

Вообще-то определение размерности векторного пространства ни с какой непрерывностью не связано. ТС: Ваши фантазии неуместны, учебники читать надо

[Red_Herring]

Munin в сообщении #907238 писал(а):

Эту связь изучает наука топология. Почитайте.

Если речь идёт о топологическом пр-ве, то действительно, есть разные топологические определения размерности—по Лебегу, по Урысону, по Хаусдорфу, по Минковскому (две последние требуют метрику и необязательно целочисленные).

Oleg Zubelevich в сообщении #907246 писал(а):

Вообще-то определение размерности векторного пространства ни с какой непрерывностью не связано. ТС: Ваши фантазии неуместны, учебники читать надо

Если речь идёт о векторном пр-ве, то есть стандартное определение.

Если речь идёт о вещественном топологическом векторном пр-ве, то все определения дают одно и то же.

_hum_ в сообщении #907169 писал(а):

Обычно, в обывательском смысле...

Ну и спрашивайте у тех, кто такие "определения" даёт.

[_hum_]

Munin в сообщении #907238 писал(а):

Эту связь изучает наука топология. Почитайте.

Та топология, основы которой я изучал, занимается вопросами топологической структуры пространства безотносительно к структуре линейного. Если вы имели в виду что-то конкретное, может, дадите ссылки на дисциплины, основные теоремы и т.п.?

Oleg Zubelevich в сообщении #907246 писал(а):

Вообще-то определение размерности векторного пространства ни с какой непрерывностью не связано. ТС: Ваши фантазии неуместны, учебники читать надо

Ок. Тогда тогда сформулирую вопрос чисто математически:
известно, что $\mathbb{R}^n$ можно биективно отобразить на $\mathbb{R}^m,\, m < n$, соответственно, алгебраическая размерность при таких отображениях не сохраняется. Так вот интересно узнать наиболее общие условия на отображение, при которых подобное было бы невозможным (биекция в этом классе отображений была возможна только между множествами одинаковых алгебраических размерностей). Когда-то давно я краем уха слышал, что, например, таким условием является непрерывность (соответственно, пространства должны рассматриваются как топологические). Если это так, то мне было бы интересно узнать, как именно непрерывность "спасает" размерность. На первый взгляд, эти понятия никак не связаны.

[Oleg Zubelevich]

_hum_ в сообщении #907259 писал(а):

известно, что $\mathbb{R}^n$ можно биективно отобразить на $\mathbb{R}^m,\, m < n$, соответственно, алгебраическая размерность при таких отображениях не сохраняется.

алгебраическая размерность сохраняется при биекциях, сохраняющих алгебраическую структуру в данном случае линейность. Векторное пространство не обязано быть конечномерным и не обязано быть наделенным какой-либо топологией и не обязано быть над полем действительных чисел. Алгебраическая размерность определена для любого векторного пространства. В $\mathbb{R}^m$ существует единственная топология согласованная с алгебраической структурой (и сколько угодно несогласованных) она является стандартной. В смысле этой стандартной топологии, $\mathbb{R}^m$ и $\mathbb{R}^n$ гомеоморфны тогда и только тогда когда $n= m$. Вы пытаетесь за раз освоить вещи, для понимания которых нужно прослушать несколько годовых курсов по разным разделам математики.

[Munin]

_hum_ в сообщении #907259 писал(а):

Та топология, основы которой я изучал, занимается вопросами топологической структуры пространства безотносительно к структуре линейного. Если вы имели в виду что-то конкретное, может, дадите ссылки на дисциплины, основные теоремы и т.п.?

Я не знаю, что вы изучали. Есть такой раздел топологии - общая топология. Иногда бегло упоминается в начале курса топологии, иногда идёт отдельным курсом. Например, есть большая книга Энгелькинг. Общая топология.

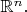
Там определения, действительно, даны безотносительно к структуре линейного пространства. Но как частный случай, рассматриваются стандартные топологии на $\mathbb{R}$ и $\mathbb{R}^n.$ После сотни страниц определений и теорем, это делается элементарно :-)

Ссылки на основные теоремы вам назвали:

Red_Herring в сообщении #907255 писал(а):

есть разные топологические определения размерности—по Лебегу, по Урысону, по Хаусдорфу, по Минковскому (две последние требуют метрику и необязательно целочисленные).

Oleg Zubelevich говорит об алгебраической размерности, это действительно отдельное понятие. Не знаю, насколько оно вам нужно. Наше пространство трёхмерно и в алгебраическом, и в топологическом (по-видимому) смысле.

[_hum_]

Oleg Zubelevich

Oleg Zubelevich в сообщении #907273 писал(а):

алгебраическая размерность сохраняется при биекциях, сохраняющих алгебраическую структуру в данном случае линейность.

Меня интересует не "тогда", а "только тогда сохраняет". Изоморфизм не является необходимым условием для сохранения (при биективном отображении) размерности пространства.

P.S. Я в курсе всех приведенных вами фактов, и в свое время "слушал разные курсы по разным разделам математики" :)

Munin, спасибо, но не могли бы вы указать, где в общей топологии касаются вопроса сохранения алгебраической размерности при гомеоморфных (не обязательно линейно изоморфных) преобразованиях линейных топологических пространств?

[Munin]

_hum_ в сообщении #907296 писал(а):

но не могли бы вы указать, где в общей топологии касаются вопроса сохранения алгебраической размерности

Не мог бы. Как вам уже сказали, есть топологическая размерность, а есть алгебраическая. В общей топологии не касаются алгебраической размерности.

[_hum_]

Munin в сообщении #907303 писал(а):

Не мог бы. Как вам уже сказали, есть топологическая размерность, а есть алгебраическая. В общей топологии не касаются алгебраической размерности.

Ну, я как бы с самого начала так и говорил - что мой вопрос вряд ли подпадает под чистую общую топологию.

-- Сб сен 13, 2014 16:07:16 --

Oleg Zubelevich, нет, не так. Постановка: есть два линейных пространства, и есть биекция между ними. Вопрос: какие есть критерии того, что эти пространства могут/не могут иметь одинаковую алгбраическую размерность при такого типа биекций.

(Например, чтобы использовать для доказательства того, что плоскость нельзя гомеоморфно отобразить на прямую)

[Oleg Zubelevich]

Я вижу только один способ вменяемо сформулировать Ваш вопрос. Имеются два линейных топологических пространства над $\mathbb{R}$. Эти пространства гомеоморфны. Вопрос: являются ли они изоморфными как линейные пространства (в чисто алгебраическом смысле)?

_hum_ в сообщении #907308 писал(а):

Например, чтобы использовать для доказательства того, что плоскость нельзя гомеоморфно отобразить на прямую

ну это просто смешно. Выбросили из прямой точку получили не линейно связное множество. Выбросили из плоскости точку -- множество осталось линейно связным.

[Munin]

_hum_ в сообщении #907308 писал(а):

Ну, я как бы с самого начала так и говорил - что мой вопрос вряд ли подпадает под чистую общую топологию.

С самого начала вы и слова-то такого не упоминали. Непрерывность изучается общей топологией. Алгебраическая размерность не имеет ничего общего с непрерывностью. Так что, я пытался понять ваш вопрос по названным вами ассоциациям.

[_hum_]

Oleg Zubelevich в сообщении #907315 писал(а):

Я вижу только один способ вменяемо сформулировать Ваш вопрос. Имеются два линейных топологических пространства над $\mathbb{R}$. Эти пространства гомеоморфны. Вопрос: являются ли они изоморфными как линейные пространства (в чисто алгебраическом смысле)?

Нет. Это не тот вопрос. Свой вопрос я сформулировал выше. Жаль, что вы не поняли.

Oleg Zubelevich в сообщении #907315 писал(а):

ну это просто смешно. Выбросили из прямой точку получили не линейно связное множество. Выбросили из плоскости точку -- множество осталось линейно связным.

А некоторые используют другой (более общий, на мой взгляд) подход - ссылаются на следствие domain invariance theorem:

Цитата:

Theorem (L. E. J. Brouwer). If $U$ is an open subset of $R^n$ and $f : U \rightarrow R^n$ is an injective continuous map, then $V = f(U)$ is open and $f$ is a homeomorphism between $U$ and $V$.

Цитата:

Consequences
$R^n$ cannot be homeomorphic to $R^m$ if $m \neq n$.

Indeed, no non-empty open subset of $R^n$ can be homeomorphic to any open subset of $R^m$ in this case.

-- Сб сен 13, 2014 17:31:20 --

Munin в сообщении #907330 писал(а):

_hum_ в сообщении #907308 писал(а):

Ну, я как бы с самого начала так и говорил - что мой вопрос вряд ли подпадает под чистую общую топологию.

С самого начала вы и слова-то такого не упоминали. Непрерывность изучается общей топологией. Алгебраическая размерность не имеет ничего общего с непрерывностью. Так что, я пытался понять ваш вопрос по названным вами ассоциациям.

Я с самого начала говорил:

_hum_ в сообщении #907259 писал(а):

Та топология, основы которой я изучал, занимается вопросами топологической структуры пространства безотносительно к структуре линейного. Если вы имели в виду что-то конкретное, может, дадите ссылки на дисциплины, основные теоремы и т.п.?

[Munin]

Это не "с самого начала", а второе сообщение.

[_hum_]

Munin в сообщении #907359 писал(а):

Это не "с самого начала", а второе сообщение.

:) ясно же, что речь шла про "с самого начала разговора с вами"

Так а все-таки, касательно моего вопроса еще какие-нибудь соображения будут. Или вы тоже объявляете его некорректным и закрываете тему?