Некоторые задачи ОТО, СТО.

[LynxGAV]

Аурелиано Буэндиа писал(а):

$L_{\xi}A^{\alpha ...}_{\ \beta ...}(x) = \begin{array}{c}- \lim \\ {\scriptstyle \epsilon \to 0} \end{array} \left\{ A'^{\alpha ...}_{\ \beta ...}(x)-A^{\alpha ...}_{\ \beta ...}(x)\right\}/\epsilon.$

Слушай, я только сейчас покосилась. В числителе-то, как я понимаю, надо сравнивать шуточку не те величины. Преобразование "протягивает" тензор $A^{\alpha ...}_{\ \beta ...}(x)$ из $P \to Q$: $A^{\alpha ...}_{\ \beta ...}(x) \to A'^{\alpha ...}_{\ \beta ...}(x')$, компоненты которого даются обычным законом преобразования тензоров. Поэтому сравнение происходит между тензором $A^{\alpha ...}_{\ \beta ...}(x')$, который уже есть в $Q$, c "протянутым" $A'^{\alpha ...}_{\ \beta ...}(x')$. Короче, штрихов не хватает.

Мда, а как правильно говорить? "Протянуть" тензор? В английском есть глагол 'drag' (along) .

[Someone]

LynxGAV писал(а):

Мда, а как правильно говорить? "Протянуть" тензор? В английском есть глагол 'drag' (along) .

Перенести (по кривой).

[AHOHbIMHO]

AHOHbIMHO писал(а):

Аурелиано Буэндиа писал(а):

Определение: Рассмотрим инфинитезимальное преобразование $x'^{\mu}=x^{\mu}+\epsilon \xi^{\mu}(x)$. Производная Ли вдоль поля $\xi^{\mu}(x)$ имеет вид
$L_{\xi}A^{\alpha ...}_{\ \beta ...}(x) = \begin{array}{c}- \lim \\ {\scriptstyle \epsilon \to 0} \end{array} \left\{ A'^{\alpha ...}_{\ \beta ...}(x)-A^{\alpha ...}_{\ \beta ...}(x)\right\}/\epsilon. $

Дописал: Коллеги, Вы придрались к обозначениям, а другую опечатку и не заметили. Исправляю знак перед пределом на минус! =))

Гы, знак, по-моему, Вы зря исправили . Было вроде правильно.

Не, все-таки, правильно исправили. Я посмотрел книжку Чандрасекара, там производная Ли определяется так, что производная Ли от скалара есть производная по направлению, такому знаку соответствует именно предел со знаком "минус".

[LynxGAV]

Аурелиано Буэндиа писал(а):

Коллеги, Вы придрались к обозначениям, а другую опечатку и не заметили. Исправляю знак перед пределом на минус! =))

Здравствуй, коллега . У тебя и был минус!

LynxGAV писал(а):

Аурелиано Буэндиа писал(а):

$L_{\xi}A^{\alpha ...}_{\ \beta ...}(x) = \begin{array}{c}- \lim \\ {\scriptstyle \epsilon \to 0} \end{array} \left\{ A'^{\alpha ...}_{\ \beta ...}(x)-A^{\alpha ...}_{\ \beta ...}(x)\right\}/\epsilon.$

К обозначениям я не придиралась, мне кажется, так писать нельзя.

[LynxGAV]

AHOHbIMHO писал(а):

Я посмотрел книжку Чандрасекара, там производная Ли определяется так, что производная Ли от скалара есть производная по направлению, такому знаку соответствует именно предел со знаком "минус".

Какая-какая там книга? Про дыры?

[AHOHbIMHO]

LynxGAV писал(а):

AHOHbIMHO писал(а):

Я посмотрел книжку Чандрасекара, там производная Ли определяется так, что производная Ли от скалара есть производная по направлению, такому знаку соответствует именно предел со знаком "минус".

Какая-какая там книга? Про дыры? (Уж не гравитационные и электромагнитные волны?)

Да, про дыры. "Математическая теория черных дыр". И у Шмутцера "Точные решения ур. Эйнштейна" посмотрел. Там определяется производная Ли в безиндексном формализме, но оно соответствует определению у Чандрасекара. Вобщем я все имеющие по ОТО книжки посмотрел, производную Ли я встретил только в этих двух (может плохо смотрел, конечно)

[LynxGAV]

AHOHbIMHO писал(а):

Да, про дыры. "Математическая теория черных дыр". И у Шмутцера "Точные решения ур. Эйнштейна" посмотрел. Там определяется производная Ли в безиндексном формализме, но оно соответствует определению у Чандрасекара. Вобщем я все имеющие по ОТО книжки посмотрел, производную Ли я встретил только в этих двух (может плохо смотрел, конечно)

Вот теперь Вы меня поняли. Меня эта производная интересует в приложении к ОТО, а в книгах ее нет. Хоть диффгем не читался, сам как-то нападал с неба и воспринимать можно, но я все же предпочитаю оставаться в своих пушистых тапочках и работать с тензорами.

[LynxGAV]

АНОНЫМНО, может мы на пару сообразим. (Аурелиано, похоже, на некоторое время смылся.)

Производная Ли общего тензорного поля $T_{b...}^{a...}$: $L_X T_{b...}^{a...}=X^c{\partial}_cT_{b...}^{a...}-T_{b...}^{c...}{\partial}_cX^a-...+T_{c...}^{a...}{\partial}_b X^c+...$.

Так как я делаю, у меня не получается положительный знак для соответствующего ковариантного индекса.

[LynxGAV]

Аурелиано Буэндиа писал(а):

Следствие 1:
$L_{\xi}A^{\alpha}_{\cdot \beta}(x) = \xi^{\mu}A^{\alpha}_{\cdot \beta, \mu}(x)- \xi^{\alpha}_{,\mu} A^{\mu}_{\cdot \beta}(x)+\xi^{\nu}_{,\beta}A^{\alpha}_{\cdot \nu}(x)$

Следствие 2:
$L_{\xi}\psi(x) = \xi^{\mu}\psi_{, \mu}(x)$

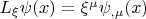Следствие 3:
$L_{\xi}A^{\alpha}(x) = \xi^{\mu}A^{\alpha}_{, \mu}(x)-A^{\mu}\xi^{\alpha}_{,\mu}\equiv[\xi,A]^{\alpha}$

Следствие 4:
$L_{\xi}L_{\eta}-L_{\eta}L_{\xi}=L_{[\xi,\eta]}$

Следствие 5:
Из $L_{\xi}g_{\alpha\beta}(x)=0$, следует уравнение Киллинга $\nabla_{[\alpha}\xi_{\beta ]}=0$

Хочешь разобраться докажи эти 5 следствий. Решай по порядку (сложность возрастает с ростом номера).

Следствие 1. Будет ясно, если учесть сообщение выше.
Следствие 2. Это производная Ли от скалярного поля $\psi$: $L_X\psi=X\psi=X^a{\partial}_a \psi$.
Следствие 3. Ничего особенного из себя не представляет, потому что является частным случаем следствия 1.
Следствие 4. Очевидно =).
Следствие 5. Надо доказывать.
Тут я бы привлекла другие сведения. По определению метрика называется форм-инвариантной при преобразовании изометрии $x^a \to x'^a$, если $g_{ab}(y)=g'_{ab}(y)$ для всех координат $y^c$. Согласно закону преобразования ковариантного тензора $g_{ab}(x)=\frac{\partial x'^c}{\partial x^a}\frac{\partial x'^d}{\partial x^b}g'_{cd}(x')$. Теперь $x^a \to x'^a$ будет изометрией, если $g_{ab}(x)=\frac{\partial x'^c}{\partial x^a}\frac{\partial x'^d}{\partial x^b}g_{cd}(x')$. Если рассмотреть инфинитезимальное преобразование координат $x^a \to x'^a = x^a + \epsilon X^a (x)$, производная которого $\frac{\partial x'^a}{\partial x^b} = {\delta}^a_b + \epsilon {\partial}_b X^a$, подставляя и опять-таки с помощью т.Т. получается: $g_{ab}(x)= ({\delta}^c_a + \epsilon {\partial}_a X^c)({\delta}^d_b + \epsilon {\partial}_b X^d)g_{cd}(x^e+\epsilon X^e) =({\delta}^c_a + \epsilon {\partial}_a X^c)({\delta}^d_b + \epsilon {\partial}_b X^d)(g_{cd}+\epsilon X^e{\partial}_e g_{cd}(x)+...) =g_{ab}(x)+\epsilon (g_{ad}{\partial}_bX^d +g_{bd}{\partial}_aX^d+X^e{\partial}_eg_{ab})+\mathcal{O}({\epsilon}^2)$. Вычитая $g_{ab}(x)$ c двух сторон, учитывая члены первого порядка малости, величина в скобках должна дать ноль, а она и есть производная Ли: $L_X g_{ab}=X^e {\partial}_eg_{ab} + g_{ad}{\partial}_bX^d + g_{bd}{\partial}_aX^d$. А теперь в выражении для производной Ли можно заменить обычные производные ковариантными и использовать ${\nabla}_c g_{ab}=0$ и $T^{...}_{..a}=g_{ab}T^{..b}_{...}$, тогда $L_X g_{ab}={\nabla}_b X_a+{\nabla}_aX^b=0$.
Кроме того, по идее, производная Ли должна быть линейной, подчиняться правилу Лейбница, сохранять тип тензора, коммутировать со сверткой. А может я не буду гадать на кофейную гущу и ты мне дашь книгу откуда ты этих свойств понабрал, не самому же тебе в голову такие обозначения приходят? И как доказательство, удовлетворительное? Может математики знают порядочную литературу по данному вопросу?

[Dolopihtis]

LynxGAV писал(а):

АНОНЫМНО, может мы на пару сообразим. (Аурелиано, похоже, на некоторое время смылся.)

Производная Ли общего тензорного поля $T_{b...}^{a...}$: $L_X T_{b...}^{a...}=X^c{\partial}_cT_{b...}^{a...}-T_{b...}^{c...}{\partial}_cX^a-...+T_{c...}^{a...}{\partial}_b X^c+...$.

Так как я делаю, у меня не получается положительный знак для соответствующего ковариантного индекса.

Прошу прощения, может мое замечание покажется тривиальным, но не является ли причиной то , что Вы забыли заменить $\frac {\partial x'^a}{\partial x^b} = {\delta}_a^b + \delta u {\partial}_b X^a$ на $\frac {\partial x^a}{\partial x'^b} = {\delta}_a^b - \delta u {\partial}_b X^a$ для ковариантных индексов.

[LynxGAV]

Dolopihtis писал(а):

Прошу прощения, может мое замечание покажется тривиальным, но не является ли причиной то , что Вы забыли заменить $\frac {\partial x'^a}{\partial x^b} = {\delta}_a^b + \delta u {\partial}_b X^a$ на $\frac {\partial x^a}{\partial x'^b} = {\delta}_a^b - \delta u {\partial}_b X^a$ для ковариантных индексов.

Нормальное замечание. $x'^a=x^a+ \delta u X^a(x)$. Отсюдa $x^a=x'^a -\delta u X^a(x')$. Пошла отдохну .

[AHOHbIMHO]

LynxGAV писал(а):

АНОНЫМНО, может мы на пару сообразим. (Аурелиано, похоже, на некоторое время смылся.)

Производная Ли общего тензорного поля $T_{b...}^{a...}$: $L_X T_{b...}^{a...}=X^c{\partial}_cT_{b...}^{a...}-T_{b...}^{c...}{\partial}_cX^a-...+T_{c...}^{a...}{\partial}_b X^c+...$.

Так как я делаю, у меня не получается положительный знак для соответствующего ковариантного индекса.

Имеем инфинитиземальное преобразование:

$${x'}^a=x^a+\epsilon X^a(x)$$ $$x^a={x'}^a-\epsilon X^a(x')$$ $$\frac{\partial {x'}^a}{\partial x^b}={\delta}_b^a+\epsilon {\partial}_b X^a(x)$$ $$\frac{\partial x^a}{\partial {x'}^b}={\delta}_b^a-\epsilon {\partial}_b X^a(x')$$

Здесь формулы написаны с точность до первого порядка малости.
Общий вид преобразования тензора имеет вид:

$${T'}_{b...}^{a...}(x')=\frac{\partial {x'}^a}{\partial x^c}...\frac{\partial x^d}{\partial x'^b}...T_{d...}^{c...}(x)$$

Напишем это преобразование с точностью до первого порядка малости:

$${T'}_{b...}^{a...}(x')=T_{b...}^{a...}(x)+\epsilon \partial_c X^a (x) T_{b...}^{c...} (x)+...-\epsilon \partial_b X^c (x') T_{c...}^{a...}(x)-...$$ $${T'}_{b...}^{a...}(x')=T_{b...}^{a...}(x)+\epsilon \partial_c X^a (x') T_{b...}^{c...} (x')+...-\epsilon \partial_b X^c (x') T_{c...}^{a...}(x')-...$$ $${T'}_{b...}^{a...}(x')=T_{b...}^{a...}(x'-\epsilon X(x'))+\epsilon \partial_c X^a (x') T_{b...}^{c...} (x')+...-\epsilon \partial_b X^c (x') T_{c...}^{a...}(x')-...$$ $${T'}_{b...}^{a...}(x')=T_{b...}^{a...}(x')-\epsilon X^c(x')\partial_c T_{b...}^{a...}(x')+\epsilon \partial_c X^a (x') T_{b...}^{c...} (x')+...-\epsilon \partial_b X^c (x') T_{c...}^{a...}(x')-...$$ $${T'}_{b...}^{a...}(x)=T_{b...}^{a...}(x)-\epsilon X^c(x)\partial_c T_{b...}^{a...}(x)+\epsilon \partial_c X^a (x) T_{b...}^{c...} (x)+...-\epsilon \partial_b X^c (x) T_{c...}^{a...}(x)-...$$ $$-{T'}_{b...}^{a...}(x)=-T_{b...}^{a...}(x)+\epsilon X^c(x)\partial_c T_{b...}^{a...}(x)-\epsilon \partial_c X^a (x) T_{b...}^{c...} (x)-...+\epsilon \partial_b X^c (x) T_{c...}^{a...}(x)+...$$ $$-({T'}_{b...}^{a...}(x)-T_{b...}^{a...}(x))=\epsilon X^c(x)\partial_c T_{b...}^{a...}(x)-\epsilon \partial_c X^a (x) T_{b...}^{c...} (x)-...+\epsilon \partial_b X^c (x) T_{c...}^{a...}(x)+...$$ $$-({T'}_{b...}^{a...}(x)-T_{b...}^{a...}(x))/\epsilon = X^c(x)\partial_c T_{b...}^{a...}(x)- \partial_c X^a (x) T_{b...}^{c...} (x)-...+ \partial_b X^c (x) T_{c...}^{a...}(x)+...$$ $$L_X T_{b...}^{a...} = X^c(x)\partial_c T_{b...}^{a...}(x)- \partial_c X^a (x) T_{b...}^{c...} (x)-...+ \partial_b X^c (x) T_{c...}^{a...}(x)+...$$

Получается, что определение производно должно выглядеть так:

$$L_X T_{b...}^{a...} = -\lim_{\epsilon \to 0}{({T'}_{b...}^{a...}(x)-T_{b...}^{a...}(x))/\epsilon$$}

[LynxGAV]

AHOHbIMHO писал(а):

Получается, что определение производно должно выглядеть так:

$$L_X T_{b...}^{a...} = -\lim_{\epsilon \to 0}{({T'}_{b...}^{a...}(x)-T_{b...}^{a...}(x))/\epsilon$$}

Спасибо , я поняла уже к тому моменту. Только не дойду зачем Вы и Аурелиано Буэндия так старательно минус выносите. Он что имеет какой-то магический смысл? (шутка) И еще я бы все-таки оставляла штрихованные координаты в определении, а в доказательстве Вы делаете замену $x \to x'$. И на будущее не стоит тратить столько времени для набора, мне можно словами пояснять, я сама люблю делать всё.

[AHOHbIMHO]

LynxGAV писал(а):

AHOHbIMHO писал(а):

Получается, что определение производно должно выглядеть так:

$$L_X T_{b...}^{a...} = -\lim_{\epsilon \to 0}{({T'}_{b...}^{a...}(x)-T_{b...}^{a...}(x))/\epsilon$$}

Спасибо , я поняла уже к тому моменту.

Я тоже понял, что уже Вы поняли. Это произошло, пока я пост писал

LynxGAV писал(а):

Только не дойду зачем Вы и Аурелиано Буэндия так старательно минус выносите. Он что имеет какой-то магический смысл? (шутка)

Почему-то до этого момента у меня в голове запомнилась формула без "минуса". Представляете, какой удар!

LynxGAV писал(а):

И еще я бы все-таки оставляла штрихованные координаты в определении, а в доказательстве Вы делаете замену $x \to x'$.

В общем-то это не существенно. Главное, что и в штрихованную, и в нештрхованную функцию подставляется один и тот же аргумент.

LynxGAV писал(а):

И на будущее не стоит тратить столько времени для набора, мне можно словами пояснять, я сама люблю делать всё.

А мне словами очень сложно К тому же упражняюь в Latex'e. До обнаружения этого форума формулы только в ворде набивать умел. А народ с мехмата надо мной смеялся, мол, это - попса .
Да, к тому же я заметил, чьл выкладки над крокодилами делать в электронном виде удобней, т.к. копипэйст очень быстро делается.

[AHOHbIMHO]

Есть какие-нибудь методы, помогающие решать уравнение Киллига? Ну о том, что коммутатор двух векторов Киллинга, тоже есть вектор Киллига(если не ноль) , я знаю. А вот что нибудь еще...?