А через оператор вида

?
Честно снова не понял. Это ведь та же самая
* операция, просто запись другая.
Который первое. Просто у Никольского законы де Моргана названы как принцип двойственности.
Ну, если уж они так названы — в чём вопрос? Хотя название вряд ли можно считать удачным, какое-то слишком глобальное. В математике много двойственностей всяких.
* очень точно — нет: например, в аксиоматике ZFC постулируется существование объединение

вообще любого семейства множеств

, не важно какой мощности, а
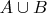
определяется как

, и

определяется как

. Т. е. тут ни одна из двух обычных записей не использует в определении другую — ни одна не «лучше»; по-человечески же это вообще
просто одно и то же.
-- Пн июн 30, 2014 02:45:47 --Единственная мое предположение, это что множество

содержит единственное действительное число

Можете укрепить его и увидеть путь к аргументам, нарисовав друг под другом несколько числовых осей с промежутками

и посмотря на последовательные объединения.
P. S.
Bonaqua, пожалуйста, набирайте формулы просто как
$что-нибудь$ — теги
math сами проставятся, а вот при их наборе доллары, включающие математический режим, сами не проставятся. В редких случаях (чертёж с помощью TikZ сделать, например) они вредны, но в основном необходимы, потому что
(1) математический режим, конечно, сам включится после встречи большинства математических команд типа
\times, но до того шрифт и типографика будут текстовые и совсем не соответствующие:

vs,

;
(2) при цитировании кнопкой

на месте формулы остаётся только её код без тегов
math, так что цитирующему приходится расставлять неуказанные доллары заново.
Вот такая просьба.

Надеюсь, вы сочтёте её обоснованной.
-- Пн июн 30, 2014 02:53:23 --Попытка расшифровки вышецитированного непонятного куска:
А через оператор вида

? Так



— это ведь одно множество

, так что если

определить равным ему, это будет просто последовательность из одинаковых значений. Объединение

, сколько бы их там не было, потому будет равно этому значений. Вряд ли вы это имели в виду?
Вы хотели сказать, что

? Такое равенство можно, конечно, переписать для любого множества:

(с индексами будет неестественно) — только цель неясна.



