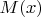
, как Вы указали в самом начале, равен единице. Так что в распечатке-то? Может, среднее по какой-то
выборке? Какой, на сколько штук?
Да, вы меня раскусили, это даже не выборочное среднее, это всего лишь единичные значения

после тысячи итераций.
Добавил усреднение по выборке объема 1000. Получил почти тоже самое.
На всякий случай, код на питоне:
http://ideone.com/6WhWT1-- 16.06.2014, 18:30 --Пусть выполнено

умножений. В среднем (не будем пока пользовать страшные термины вроде "матожидания") число будет умножено

раз на

и

же раз - на

. Тем самым оно будет уможено на

, что при

, очевидно, стремится к нулю. И чему же Вы удивляетесь?
То что произведение стремится к нулю вроде понятно. Но ведь и матожидание тоже должно стремиться к нулю? Почему оно не стремится? Или я не правильно посчитал?



