Он действует так:

Откуда берется здесь обязательно коеффициент

?
По меньшей мере если новая частица различимая (т.е. "добавляем электрон" к "однопротонном состоянии") то это как-бы не стыкуется с тем, что меня в этой теме до сих пор "учили".
Например в выкладок Munin с умножением на дельта-функций, никаких добавочных коеффициентов не было.
(также "на пальцах", для частного случая, рассуждаю так - допустим для простоты, что возможные состояния - базис - для частиц, это либо в левой половины интервала [0,1], либо в правой половины интервала [0,1]. Допустим первая частица-протон, находится "чисто" где-то в левой половины; нормированность требует чтобы квадрат коеффициента был равен 1. Пусть вторую частицу-электрон вводим так же в чистом состоянии в "левой половины", то же самое для ее квадрата коеффициента. Тогда для двухчастичном состоянии обоих частиц находящихся в четвертинку "квадрата" [0,1]x[0,1] фазового пространства простым перемножением получаем что коеффициент двухчастичного состояния чтобы находится в нижней-левой четвертинки равен 1*1=1; т.е. все и так нормированно для двухчастичной ф-и амплитуды вероятности, и без всяких дополнительных коеффициентов - во всех случаев сумма вероятностей чтобы частицы находились "где-то", равна 1.
Если рассуждать интегралами плотности вероятности величина ступеньчатой функции в [0,0.5] на интервале [0,1] получается 2 а величина на квадратике [0,0.5]x[0,0.5] в квадрате [0,1]x[0,1] фазового пространства будет 4 и опять простое перемножение достаточно, безо всяких дополнительных коеффициентов.)
Тут еще стоит сказать, что я [думаю, что!] понимаю откуда и как этот коеффициент берется в изложении ФЛФ Фейнмана (КМ 1 Том 8, пар. 2 "Состояния с двумя бозе частицами" и далее) - но там впервых смысл значков кажется несколько другим, во вторых у него вроде речь идет конкретно про бозонов (т.е. неотличимых частиц); a вы пишете что это только "
далее обычно нужно учесть".
Для развлечения давайте вычислим подобным способом как действует оператор уничтожения на двухчастичное состояние

.

Тут не совсем понятно, если прямо в лоб то коеффициент

вроде должен выскочить дважды и получиться

- так как мы "дважды прилагаем" это разложение (а вектор базиса

"такой же как и все другие")?
В первом слагаемом одночастичное состояние (коммутатор --- просто число).
Почему коммутатор - просто число, а не оператор?
-- 04.05.2014, 22:55 --Если хотите понять, что будет с функциями, то напишите более общее состояние, например:

подействуйте оператором (обобщенно обозначим

--- это любой оператор) и протащите этот оператор до базисного вектора:

Для такого "протаскивания" ничего не нужно делать - это следует просто из линейности оператора - это верно?
Далее можно переразложить

по координатным базисным векторам (для "координатного" оператора уничтожения так сразу получится, фактически ничего не надо делать) и получить выражение исходного (до действия оператора) типа, но с преобразованными коэффициентами.
Это в принципе понятно для "любого оператора" но не и для конкретных случаев .
Для этого все же нужно знать, как этот "любой оператор", действует на векторы из базиса... Допустим это "оператор уничтожения"
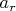
, что тогда "сразу получится" - как "преобразуются коеффициенты", и почему; откуда придет корень двойки?



