|
|
drowsy писал(а): О чём можно на 9 страницах разговаривать с человеком, который в математике в 3-х соснах путаеться ? AD писал(а): Заметьте, что страниц не 9, а гораздо больше - есть еще старая, ныне закрытая, тема, там тоже страниц 10 Больше! Эта статистика к темам не относится. Спасибо всем, кто наставлял меня на уточнение истины. Нежелание математиков исправлять ошибку в понятии числа, я предсказал в самом начале входа на Форум. Этот процесс требует времени. Время нас и рассудит.
STilda писал(а): Кроме того, уверяю вас, представление систем чисел в виде  очень сильно затрудняет нахождение соответствия этим системам в реальности и физике.  - это нормально, так как это модели, соответствующие природному определению числа, которое формировалось тысячелетиями. Но оно не должно существовать само по себе, как и все мы. А - это нормально, так как это модели, соответствующие природному определению числа, которое формировалось тысячелетиями. Но оно не должно существовать само по себе, как и все мы. А  должно быть носителем значений из должно быть носителем значений из  . Тогда будет полный порядок. . Тогда будет полный порядок.
Добавлено спустя 3 минуты 46 секунд:Последняя редакция.
Элементарное доказательство теоремы ВТФ для треугольника
Теорема (ВТФ для треугольника). Пусть  означает, какое угодно, целое положительное число и означает, какое угодно, целое положительное число и  , тогда для прямоугольного треугольника со сторонами , тогда для прямоугольного треугольника со сторонами  , имеет место соотношение , имеет место соотношение

ДоказательствоПусть  - искомый прямоугольный треугольник с прямым углом - искомый прямоугольный треугольник с прямым углом  , противолежащего стороне , противолежащего стороне  . Введем обозначения: . Введем обозначения:

Тогда

Возводя, левые иправые части, в степень  и подставляя в соотношение (1) вместо и подставляя в соотношение (1) вместо  , соответственно , соответственно , получим , получим

По теореме косинусов, для всякого треугольника [5, 330], со сторонами (3) и соответствующими им углами имеют место соотношения

При этом, для сторон треугольника, должны выполняться условия

которые, согласно (3) и условия теоремы, выполняются. А для углов треугольника должны выполняться свои условия:

которые, согласно условию теоремы также выполняются. Подставляя  в первое из соотношений (5), получим в первое из соотношений (5), получим

Первое из этих соотношений совпадает с (4), а второе и третье (с учетом соотношений между сторонами и углами прямоугольного треугольника), являются его производными. Теорема доказана.
Следствие 1. Для треугольника, отличного от прямоугольного, соотношение (4) место не имеет. Доказательство следует из соотношений (5), так как, в этом случае  отличны от нуля. отличны от нуля.
Следствие 2 (ВТФ для отрезка). При отсуствии треугольника, соотношение (3) место не имеет.
Доказательство. Полагая в соотношениях (7)  , получим три одинаковых соотношения , получим три одинаковых соотношения

совпадающим с уравнением Ферма, но противоречащим условиям (6) и, которое, одновременно с (4) выполняться не может.
Теорема (Треугольник для ВТФ). Если для, отличных от нуля  и положительного целого и положительного целого  выполняется соотношение выполняется соотношение

причем векторы  не коллинеарны, тогда существует хотя бы один треугольник со сторонами не коллинеарны, тогда существует хотя бы один треугольник со сторонами

Доказательство. Представим  и и  в тригонометрической форме [4, 13] в тригонометрической форме [4, 13]
 , ,
где
 -модули, -модули,  - значения аргументов - значения аргументов  и и  соответственно. соответственно.
Подставим (11) в соотношение (10), тогда, после возведения в степень  , получим , получим
 . .
Приравнивая отдельно действительные и мнимые части, получим

Возводя оба соотношения (12) в квадрат, и складывая, отдельно левые и правые части, получим

Переписав уравнение (10) в виде

и проделав с этим уравнением такую же процедуру, как и с уравнением (10), получим
 . .
Аналогично, для уравнения

Получим
 . .
Объединив соотношения (13) – (15) в виде системы, получим условия
совместности для модулей векторов и углов уравнения (10):

где

Из (17) следует, что

Соотношения (16) совпадают с соотношениями (4), следовательно они определяют для шестерки величин  и и 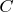 теорему косинусов [5, 330]. теорему косинусов [5, 330].
Без умаления общности, можно допустить, что для аргументов выполняются неравенства (см. рис. 1)

В силу требований теоремы, ось отсчета аргументов выберем так, чтобы векторы  и и  находились по одну сторону от нее и все углы отсчитывались против часовой стрелки. Согласно (10) вектор находились по одну сторону от нее и все углы отсчитывались против часовой стрелки. Согласно (10) вектор  также будет лежать по туже сторону оси отсчета. Тогда будут выполняться неравенства также будет лежать по туже сторону оси отсчета. Тогда будут выполняться неравенства

В силу (17) для углов  и и 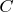 , с учетом (18), (19) и (20) будут выполняться аналогичные неравенства , с учетом (18), (19) и (20) будут выполняться аналогичные неравенства

По определению модуля, имеем очевидные неравенства:

Условия (16), (21) и (22) выполняют все требования теоремы о существовании единственного треугольника [5, 333] для шестерки величин
 . Следовательно, эти величины являются элементами треугольника. Теорема доказана. . Следовательно, эти величины являются элементами треугольника. Теорема доказана.
Следствие 1.(Теорема Пифагора, обобщение). Если угол между векторами  и и  уравнения (10) равен уравнения (10) равен  , т. е. , т. е.  , то для модулей векторов имеет место соотношение , то для модулей векторов имеет место соотношение

Доказательство. Полагая в первом соотношении (16)  , получим , получим  и первое равенство из соотношений (16) перейдет в (23). Следствие доказано. и первое равенство из соотношений (16) перейдет в (23). Следствие доказано.
При  , из равенства (23) мы получим обычную теорему Пифагора. Таким образом теорема косинусов в комплексной плоскости при условиях теоремы имеет вид: , из равенства (23) мы получим обычную теорему Пифагора. Таким образом теорема косинусов в комплексной плоскости при условиях теоремы имеет вид:

Если же угол между векторами  и и  буде равен буде равен  , то это соотношение будет теоремой Пифагора. , то это соотношение будет теоремой Пифагора.
Следствие 2. (Отрезок для ВТФ). Для уравнения Ферма не существует ни одного треугольника.
Доказательство. Для получения уравнения ВТФ, положим, в нарушении условия неколлениарности, в первом соотношении (16)  , тогда , тогда  и все три соотношения (16) примут вид: и все три соотношения (16) примут вид:

совпадающим с (9) и с уравнением Ферма. Следствие доказано.
Следствие 3. Формулировка ВТФ не корректна. Доказательство. Сравнивая формулировки теорем: треугольник для ВТФ, Пифагора и ВТФ; заключаем, что первые две сформулированы для треугольника. В формулировке ВТФ никакого геометрического образа не задано, что гарантирует ее недоказуемость для любого натурального  . .
Следствие доказано.
Выводы: 1). Решение алгебраического уравнения, независимо от нашего желания, связано с областью, для которой это уравнение определено;
2). Область, для которой это уравнение определено, находиться из условий совместности (16) для модулей, входящих в это уравнение неизвестных, и коэффициентов при них, путем раасмотрения его в комплексной плоскости;
3). Утверждать, что уравнение

при  имеет целые решения, а при имеет целые решения, а при  - действительные в условиях ВТФ ошибочно, ибо эти решения действительны только для прямоугольных треугольников, которых в условии ВТФ нет; - действительные в условиях ВТФ ошибочно, ибо эти решения действительны только для прямоугольных треугольников, которых в условии ВТФ нет;
4). Отсюда же следует, что нахождение числового примера целочисленного решения уравнения Ферма, для произвольного натурального  (в частности (в частности  ), не будет являться опровержением ВТФ. ), не будет являться опровержением ВТФ.
5). Все, имеющиеся частные случаи доказательства ВТФ ошибочны, ибо они, без всякого изменения, могут быть использованы для доказательства ВТФ, сформулированной корректно: Теорема Ферма (Корректная формулировка). Если  означает какое угодно целое положительное число, большее нежели 2, то не существует прямоугольного треугольника с катетами означает какое угодно целое положительное число, большее нежели 2, то не существует прямоугольного треугольника с катетами  и гипотенузой и гипотенузой  для которых соотношение (14) выполнялось бы при целых положительных для которых соотношение (14) выполнялось бы при целых положительных  и и  . Причем можно обобщить и на . Причем можно обобщить и на  . Таким образом, в них доказано, что среди пифагоровых троек . Таким образом, в них доказано, что среди пифагоровых троек  , для , для  , нет целых , нет целых 
Больше ничего особенного в ВТФ нет. Нет в ней никаких кривых Таниямы. Но у математиков есть проблема с аксиоматическим определением понятия числа. Определение числа, данное Пифагором – правильное! При таком определении проблема ВТФ не возникла бы, а вышеуказанные выводы не противоречили бы теории. Чтобы убедиться в этом, достаточно рассматривать задачи в комплексной плоскости. Это реально существующая модель плоской области для реальных моделей чисел (вещей), определенных по Пифагору.
Всем математических успехов!  Yarkin. Yarkin.
Литература
1. Постников М.М. Введение в теорию алгебраических чисел. М., «Наука», 1982, с.240.
2. Клейн Ф. Элементарная математика с точки зрения высшей, т.1, 4 – ое издание, М., “Наука”, 1987, с. 432.
3. Хинчин А. Я. Великая теорема Ферма, Госиздат, М – Л, 1927, с. 76.
4. Маркушевич А. И. Краткий курс теории аналитических функций, 4-ое издание, М., Наука”, 1978, с. 416.
5. Новоселов С. И. Специальный курс тригонометрии, “Советская наука”, М., 1953, с. 464.
|
|