План.
A] Формулировка теоремы Ферма и объяснение модулярного подхода.
B] Вспомогательные утверждения.
C]

D]

D1] общий случай без удвоения
D2] случай числа Софи Жермен
D3] общий случай
E] простое
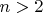
F] гипотеза Биля
A] Формулировка теоремы Ферма и объяснение модулярного подхода.

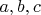
- натуральные, не имеющие общего делителя(его сокращаем),
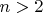
Введём замену

без переобозначения по следующему алгоритму (лишнюю часть степени спрячем в основании):
1) если

- простое, то оставим без изменений;
2) если

, то

;
3) если

- составное и

, то

,
где

-простой, нечётный, минимальный делитель

.
В практике многовековых поисков простого доказательства именно этой теоремы Ферма следует
выделить два основных подхода:
1) рассмотрение разбиения

на несколько вариантов по некоторому целочисленному признаку и
попытки доказать невозможность каждого из них, прийти к логическому противоречию;
2) переход к рациональному виду

, чаще всего делением обоих частей на правую часть,
и попытки доказать иррациональность всех решений геометрическими, тригонометрическими
или иными способами.
Рассматривать

будем по модулю

,

-натуральное.

Особенностью предлагаемого модулярного подхода является совпадение двух вышеописанных
подходов. По модулю понятия целого числа и рационального числа совпадают, а иррациональное
число является само по себе логическим противоречием. Здесь операция извлечения корня приводит в некоторых случаях к нарушению логики.
При рассмотрении разобъём область допустимых значений на зону теоремы Эйлера(обобщения малой теоремы Ферма)

и зону исключений, где

Выделим множители-исключения из зоны теоремы Эйлера, произведя замену без переобозначения.

С учётом отсутствия общего делителя в

, выберем в качестве

ту переменную, которая имеет множитель

,

. При


выберем с множителем

.
Если

не имеет множителя

, то выберем в качестве

переменную, имеющую этот множитель,или произвольную из ещё свободных в противном случае.
Третью переменную обозначим

. В итоге получаем следующее:


,

;

,

,

,

или

;

в

;
если

, то

или если

, то

в

;

,

,

.
Произведём сдвиг модифицированной тройки Ферма на функцию Эйлера. Как и в дальнейшем при рассмотрении гипотезы Биля, произведём разложение с помощью введения
иррационального в общем случае множителя и покажем отсутствие рациональных корней уже в

.
B] Вспомогательные утверждения.
1. Разложение полинома

, при

, где

-простое.




2. Лемма

:

неразложимо, если

-простое.
Доказательство через критерий Эйзенштейна. Большая благодарность уважаемому Sonic86 c форума dxdy.ru за предоставленную ссылку на доказательство.
В]

Рассмотрим

. Замена

,

,

,













Используем

.


, иррационально в

.
1)




, противоречие
2)

,





, противоречие
решений нет (метод мат. индукции)
-- 23.04.2014, 05:42 --Уважаемые форумчане, пожалуйста, покритикуйте случай

. Если здесь обнаружутся неисправимые ошибки, то с остальным будет совсем беда.



