Колебательное движение

[nikvic]

Для того же, для чего иногда считают дюжинами
Измеряя пульс, число 3.1415 не используют...

[arseniiv]

Pineapple в сообщении #794318 писал(а):

А для чего помимо обычной частоты вводится циклическая частота?

Для начала, её удобно подставлять в тригонометрические функции: $\sin(\omega t+\varphi_0)$ vs. $\sin(2\pi\nu t+\varphi_0)$. Для конца вы уже спрашивали в начале темы: для вращения она аналогична угловой скорости.

[Munin]

Pineapple в сообщении #794318 писал(а):

А для чего помимо обычной частоты вводится циклическая частота?

К тому, что уже сказали в ответ (всё очень верно), добавлю, что это пример ситуации, когда можно делать по-разному, и выбирают какой-то один вариант, более-менее удобный.

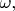
Есть разные физические величины, связанные с частотой множеством формул. И вот так получилось, что одни физические величины связаны более напрямую с обычной частотой $\nu,$ а другие - с циклической $\omega.$ Разумеется, всё, что выражается через $\omega,$ можно выразить через $\nu,$ и наоборот. Но при этом в формулах возникают коэффициенты $2\pi$ и $1/(2\pi),$ которые, честно говоря, мешаются и мозолят глаз :-) Можно их "гонять" из одних формул в другие, выбирая в качестве основной используемой величины либо обычную частоту $\nu,$ либо циклическую $\omega.$ Но это как паста в закрытом тюбике: нажмёшь в одном месте - вылезет в другом.

Поэтому выбирают, глядя по тому, какие формулы больше используются. arseniiv правильно пишет, что $\sin(\omega t+\varphi_0)$ выглядит куда красивей, чем $\sin(2\pi\nu t+\varphi_0),$ но главное даже не это. Главное - то, что эти синусы - это на самом деле решения уравнений.

В школе обычно эту тему особо не затрагивают, но то, что в школе решают как уравнения - алгебраические уравнения, тригонометрические уравнения, и их близкие аналоги (например, уравнения по модулю) - это всего лишь как первый этаж башни. Эти уравнения устроены так:
- задана функция (обычно формулой) - надо найти число.
Здесь функция играет роль условия, наложенного на число (типа $f(x)=0$), и решение уравнения состоит в том, чтобы найти число ($x$), которое этому условию удовлетворяет. А бывают уравнения другого типа, которые устроены так:
- задано условие на функцию - надо найти функцию.
Как видите, это уже "следующий этаж иерархии" (записывается в обобщённом виде иногда как $F[f(x)]=0$ или $\mathcal{F}[f(x)]=g(x),$ надо найти $f(x)$). Такие уравнения - это чаще всего дифференциальные уравнения, весьма часто встречаются также интегральные уравнения, и бывают изредка функциональные уравнения общего вида (и я не всё перечислил). Разумеется, в математике, как только придумали иерархию, можно не останавливаться, и продолжать её:
- задано условие на условие на функцию - надо найти условие на функцию ("3-й этаж");
- задано условие на условие на условие на функцию - надо найти условие на условие на функцию ("4-й этаж");
- ... и так далее.
Но на практике такие уравнения начинают встречаться уже реже, чем уравнения "2-го этажа" (а вот "2-й этаж" - чаще "1-го", имейте в виду!). Хотя когда как. Примеры уравнений "3-го этажа" - это вариационные уравнения и операторные уравнения. Операторные уравнения очень сильно используются в квантовой физике, физике элементарных частиц, физике твёрдого тела (это наиболее развитая из веток физики внутреннего устройства вещества). Это всё старшие курсы вуза и аспирантура, научная работа. Уравнения "4-го этажа" я вообще ни разу не встречал в жизни, разве что только они были где-то в неявном виде, и я их не узнал.

Всё это отступление мне понадобилось, чтобы сказать, что $\sin(\omega t+\varphi_0)$ - это решение некоторого дифференциального уравнения, обычно вот такого:

$$\dfrac{d^2x}{dt^2}=-\omega^2x\qquad\text{или}\qquad m\dfrac{d^2x}{dt^2}=-kx,$$

и вот в таком дифференциальном уравнении удобно пользоваться именно циклической частотой - именно циклическая частота входит в него совершенно естественно, как коэффициент, а не обычная. Связано это с тем, что наклон графика $\sin x$ в нуле - единица, то есть 45°. Если мы "сожмём" синус так, чтобы его период был равен единице, то есть запишем $\sin 2\pi x$ - то мы "испортим" наклон в нуле. А дифференциальное уравнение устроено таким образом, что синус весь, целиком весь бесконечный график, "вырастает" из этого наклона в точке 0, как растение из ростка. 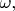Поэтому этот наклон оказывается чрезвычайно важен, и раз уж мы работаем с ним, то нам удобней величина $\omega,$ а не $\nu.$ Ещё один пример аналогичного соглашения - это когда мы получаем функцию вида $a^x$ как решение дифференциального уравнения вида

$$\dfrac{dy}{dx}=ky,$$

и вот здесь нам тоже удобно рассматривать наклон в точке 0, и взять его равным единице. Если мы его берём равным единице, то получаем экспоненту $e^x,$ $e=2{,}718\ldots,$ хотя казалось бы, просто для функции удобней было бы взять число круглое, 2 или 10. Но нет, удобней брать именно это некруглое число $e$ - для дифференциального уравнения оно оказывается "более круглым". В физике это встречается, например, там, где вычисляют период полураспада радиоактивных элементов, распадающихся ядер - по основанию 2 - и переходят от периода полураспада к другой физической величине, называемой время жизни (или иногда "среднее время жизни"), которая оказывается как раз по основанию $e.$

[Pineapple]

А почему ускорение максимально в амплитудном состоянии, скорость ведь равна 0? И какое ускорение рассматривают при колебании математического и пружинного маятника?

[nikvic]

В амплитудном состоянии пружина (или что там есть) деформирована максимально - стал быть, и "возвращаюшая сила" имеет наибольший модуль.

[Zai]

(Оффтоп)

Цитата:

Помогите с колебательным движением. Не могу разобраться...

Попрыгай на батуте - это дешево.

[Toucan]

Zai в сообщении #808347 писал(а):

Попрыгай на батуте - это дешево.

Zai, замечание за фамильярность и за неправильное цитирование.

[arseniiv]

Munin в сообщении #794397 писал(а):

В физике это встречается, например, там, где вычисляют период полураспада радиоактивных элементов, распадающихся ядер - по основанию 2 - и переходят от периода полураспада к другой физической величине, называемой время жизни (или иногда "среднее время жизни"), которая оказывается как раз по основанию $e.$

Кстати, это $e$ можно объяснить как-нибудь в обход нахождения интеграла, связанного с матожиданием экспоненциального распределения?

[nikvic]

arseniiv в сообщении #810223 писал(а):

Кстати, это $e$ можно объяснить как-нибудь в обход нахождения интеграла, связанного с матожиданием экспоненциального распределения?

Берём время, за которое распадается малая доля, и делим на эту долю.
Далее читаем про второй замечательный предел

[arseniiv]

Неочевииидно (или лень просто). Я лучше интеграть буду.