Факторизация - это, грубо говоря, когда мы имеем некоторое множество объектов, а затем постулируем, что некоторые из них "равны". При этом объекты разбиваются на классы "равных" и в дальнейшем мы на самом деле работаем с этими классами.
Например, рассматривали мы кольцо многочленов от одной переменной
![$\mathbb{R}[x]$ $\mathbb{R}[x]$](https://dxdy-04.korotkov.co.uk/f/f/1/5/f15addcc8ab3f7f3bd7b44966280b59582.png)
, в которые могу входить любые степени переменной. Факторизовать его по соотношению

(моя терминология тут, полагаю, не совсем точна) - это значит считать, что

можно заменять на 1. При этом пространство становится конечномерным, так как можно всегда избавиться от высоких степеней переменных, когда они появляются (например, при умножении).
Добавлено спустя 25 минут 13 секунд:
Я не очень понимаю пост
tolstopuz'а про тернарные операции. Давайте, изложу свое видение Вашей "Системы-1", а Вы подумайте, с чем не согласны.
Итак, мы рассматриваем множество троек неотрицательных вещественных чисел

. Буду для краткости эти объекты называть
т-числами.
Для наглядности записи мы ввели абстрактные буквы

и договорились записывать т-число

в виде суммы

. При этом значок "+" в этой записи пока что никакого содержательного смысла не имеет, это просто такой разделитель, аналогично запятой в записи

.
Строго говоря, если мы напишем просто

, то это не является т-числом, у нас еще не введено такого объекта. Но мы (опять-таки для удобства)
договорились, во-первых, не писать коэффициент 1 перед буквами, а также опускать буквы, перед которыми стоят нулевые коэффициенты. Таким образом, когда мы пишем

, то подразумеваем на самом деле т-число

или тройку

. Когда пишем

, то подразумеваем тройку

. Когда пишем 0, то подразумеваем

или тройку

.
Также мы договорились, что в записи в виде суммы "слагаемые" можно писать в любом порядке. Т.е. тройка

может быть записана и как

, и как

.
Заметьте, что пока что мы ни словом не обмолвились о том, что наши т-числа можно как-то складывать. Мы не можем утверждать, что т-число

, которое можно записать как

, есть "сумма" т-чисел

и

.
Пока что мы только обсудили некоторые способы изображения на письме элементов нашего множества

, но никаких операций на нем еще не вводили.
Теперь мы хотим определить на нашем множестве операции "сложения" и "умножения". Для того, чтобы не путаться, определим их на каноническом способе изображения. Так, мы по определению полагаем:


После того, как эти определения даны, все остальные базовые свойства (дистрибутивность, коммутативность, ассоциативность) уже проверяются. Также проверяется, что тот значок "+", который мы использовали для наглядной записи т-чисел, действительно соответствует введенной нами операции, т.е. что т-число

действительно можно рассматривать как сумму трех т-чисел

,

,

. Проверяется, что т-число
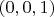
выступает в роли единицы, а т-число

выступает в роли нуля. Проверяется, что введенные операции можно выполнять "почленно", перемножая отдельные одночлены и пользуясь таблицей умножения

...
Добавлено спустя 20 минут 21 секунду:
Ну и также мы еще объявили, что т-число

и

- это одно и то же. Это уже определенная факторизация, т.е. теперь какие-то числовые тройки у нас будут обозначать одинаковые т-числа.
Теперь кратко поясню, как получить ту же самую систему по-другому. т-число

играет роль единицы (а тройки вида

в точности соответствуют обычным вещественным числам). Поскольку

, то совершенно ествественно сопоставить букве

абстрактную переменную

, тогда букве

соответствует

и мы приходим к обычным многочленам
![$\mathbb{R}[x]$ $\mathbb{R}[x]$](https://dxdy-04.korotkov.co.uk/f/f/1/5/f15addcc8ab3f7f3bd7b44966280b59582.png)
. Чтобы было выполнено

, нужно положить в этом кольце

, что я и предлагал первой факторизацией. При этом равенство

уже получается автоматически:

. Т.е. мы получили объект, в точности изоморфный т-числам, если не считать последней введенной операции.
Чтобы теперь иметь

, нужно положить

. Это - вторая факторизация, которую я предлагал. Но
AD совершенно справедливо заметил, что многочлен

делится на

. Это значит, что если мы сразу начнем с того, что положим

, то соотношение

будет выполнено автоматически. Достаточно только одной этой факторизации.
(Иными словами, достаточно постулировать следующие свойства:

является единицей,

и

. Вся остальная часть таблицы умножения выводится из них).
Итак, теперь мы в точности построили объект, соответствующий т-числам. Но заметим, что над

многочлен

неприводим. Это означает на самом деле, что у нас нет делителей нуля. Но тогда мы по теореме Фробениуса обязаны получить множество комплексных чисел.
Итак, т-числа изоморфны полю комплексных чисел относительно операций сложения и умножения, которые мы ввели. Это означает, что имеется взаимно-однозначное соответствие между т-числами и обычными комплексными числами, причем согласованное с операциями. Формулы я приводил. Можете проверять, если хотите, но это действительно так. "Система-1" =

.