Пусть

- конечное расширение числовых полей,
![$[K:F]=n$ $[K:F]=n$](https://dxdy-04.korotkov.co.uk/f/b/9/9/b995efc6642a3030cf96b0f7bc0c974682.png)
.
Пусть

, где

- целое алгебраическое число.
Пусть

- кольцо всех целых алгебраических чисел поля

.
Пусть

- кольцо всех целых алгебраических чисел поля

.
Мы доказали, что относительная дифферента

является делителем идеалов

для всех таких целых алгебраических чисел

, что

, где

- относительный минимальный полином числа

.
Докажем теперь, что

является наибольшим общим делителем этих идеалов.
Сначала докажем, что идеал

содержится в кольце

и содержит любой идеал (поля

), содержащийся в этом кольце.
Затем докажем, что для любого простого идеала

кольца

существует такое целое алгебраическое число

, что

и идеал

не делится на

.
Из этого следует, что все идеалы

(при различных

) не имеют общего простого делителя

, следовательно относительная дифферента

является наибольшим общим делителем идеалов

.
Лемма
----------
Пусть

- какое-либо целое алгебраическое число, такое, что

.
Пусть

- относительный минимальный полином числа

.
Идеал

является наибольшим идеалом кольца

, содержащимся в кольце

.
То есть идеал

содержится в кольце

и содержит любой идеал (поля

), содержащийся в этом кольце.
Доказательство
--------------------
Поскольку

, то:
(1) идеал

содержится в кольце

.
Пусть

- какой-либо идеал кольца

, содержащийся в кольце

.
Поскольку

, то

, следовательно

(поскольку

), следовательно:
(2)

.
Поскольку

является наибольшим дробным идеалом (поля

), все элементы которого имеют относительный след, принадлежащий

, то из (2) следует:
(3)

.
Из (3) следует

, значит:
(4) идеал

содержится в идеале

.
Включения (1) и (4) это то, что и требовалось доказать.
Лемма
--------------
Пусть

- какое-либо целое алгебраическое число, такое, что

.
Пусть

- относительный минимальный полином числа

.
Тогда

Доказательство
---------------------------
Поскольку

, то

, где последнее включение следует из предыдущей леммы.
Значит

, что и требовалось.
Лемма
---------------
Пусть

- какой-либо простой идеал кольца

.
Существует такое целое алгебраическое число

, что:
1)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

),
2)

по модулю идеала

.
Доказательство
---------------------------
Поскольку фактор-группа по сложению

(с операцией умножения смежных классов) является конечным полем, то множество его ненулевых элементов
является циклической группой по умножению.
Пусть смежный класс

является генератором этой циклической группы, где число

принадлежит кольцу

.
Тогдa число

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

)
Если

по модулю идеала

положим
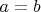
.
Пусть

по модулю идеала

.
Тогда положим

, где

- какое-либо число, принадлежащее идеалу

, но не принадлежащее идеалу

.
Поскольку

по модулю идеала

, и

- генератор мультипликативной группы по модулю идеала

, то условие 1) выполняется.
Поскольку

по модулю идеала

, то:
(5)

по модулю

.
Мы использовали разложение выражения

с биноминальными коэффициентами и то, что (биноминальный коэффициент)

делится на

(поскольку норма

равна степени простого числа, делящегося на идеал

).
Поскольку

по модулю

, то из (5) следует условие 2), что и требовалось.
Лемма
---------------
Пусть

- какой-либо простой идеал кольца

.
Пусть

- какой-либо идеал кольца

, не делящийся на

.
Существует такое число

, что:
1)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

),
2)

по модулю идеала

.
Доказательство
---------------------------
Согласно предыдущей лемме существует такое целое алгебраическое число

, что:
(6)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

) и
(7)

по модулю идеала

.
Поскольку идеалы

и

- взаимно-просты, то

, следовательно существуют такие числа

и

, что:
(8)

.
Из (8) следует, что

по модулю идеала

, следовательно из (6) следует условие 1).
Из (8) также следует, что

по модулю идеала

, следовательно из (7) следует условие 2), что и требовалось.
Лемма
---------------
Пусть

- какой-либо простой идеал кольца

.
Пусть

- какой-либо идеал кольца

, не делящийся на

.
Существует такое число

, что:
1)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

),
2)

по модулю идеала

,
3)

.
Доказательство
---------------------------
Согласно предыдущей лемме, существует такое число

, что:
(9)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

) и
(10)

по модулю идеала

.
Из доказательства теоремы о примитивном элементе:
(11)

для всех

, кроме конечного числа значений

.
Пусть
(12)

, где

- такое целое положительное число, делящееся на идеал

, что

.
Из (11) следует, что такое число

cуществует (поскольку имеется бесконечное колличество целых положительных чисел, делящихся на идеал

).
Поскольку

и

, то из (12) следует:

.
Из (12) следует, что

по модулю идеала

, следовательно из (9) следует условие 1).
Из (12) следует, что

по модулю идеала

, следовательно из (10) следует условие 2).
Поскольку из

, следует

то из (12) следует условие 3), что и требовалось.
Лемма
---------------
Пусть

- какой-либо простой идеал кольца

.
Пусть

- такое целое алгебраическое число (принадлежащее кольцу

), что:
1)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

),
2)

по модулю идеала

.
Пусть

- какое-либо целое положительное число.
Для любого целого алгебраического числа

: существует такое число

, что

по модулю идеала

.
Доказательство
---------------------------
Пусть число

.
Тогда

и

.
Пусть множество чисел

.
Тогда

- полная система вычетов по модулю идеала

.
Согласно одной из доказанных ранее теорем, множество

чисел вида

, где

, ...,

- числа из

, образуют полную систему вычетов по модулю идеала

.
Следовательно, для любого целого алгебраического числа

: существует такое число

, что

по модулю идеала

.
Множество чисел

содержится в кольце

, следовательно

, что и требовалось.
Теорема
----------------
Пусть

- какой-либо простой идеал кольца

.
Пусть

- такое целое алгебраическое число (принадлежащее кольцу

), что:
1)

- генератор мультипликативной группы по модулю идеала

(то есть числа

,

, ...,

несравнимы друг с другом по модулю

),
2)

по модулю идеала

,
3)

.
Пусть

- относительный минимальный полином числа

.
Тогда идеал

не делится на идеал

.
Доказательство
-----------------------------
Предположим обратное:
(13)

делится на идеал

.
Из (13) следует:
(14)

делится на идеал

.
Пусть

- простой идеал кольца

под идеалом

.
Пусть
(15)

, где

- целое положительное число и идеал

не делится на идеал

.
Пусть

- какое-либо число, принадлежащее идеалу

и одновременно кольцу

(такие числа существуют, например

или

).
Из

и (14) следует:
(16)

.
Поскольку

и

, то из (16) следует:
(17)

.
Пусть
(18)

, где

- целое положительное число и идеал

(кольца

) не делится на идеал

.
Существует такое целое положительное число

, что:
(19)

, где число

,
то есть

является главным идеалом (известный факт, который мы пока не доказали).
Докажем, что идеал (кольца

)

содержится в кольце

.
Из (15), (18) и (19) вместе следует:
(20)

.
Поскольку

, то:
(21)

.
Из (20) и (21) следует:
(22)

.
Из

следует

, значит:
(23)

.
Из (22) и (23) следует:
(24)

, что и требовалось.
Поскольку для любого числа

:

, где в силу предыдущей леммы можно взять такое число

, что

, то из (24) следует:
(25)

.
Поскольку любой идеал (кольца

), содержащийся в кольце

содержится в идеале

, то из (25) следует:
(26)

.
Поскольку

по предположению, то из (26) следует:
(27)

,
в противоречии с тем, что числа

и

не принадлежат простому идеалу

.
Число

не принадлежит идеалу

в силу условия 1).
Покажем, что число

не принадлежит идеалу

.
Из (18) и (19) следует, что идеал

не делится на идеал

, следовательно:
(28)

Поскольку

и

, то из (28) следует, что

, что и требовалось.



