Представляю вам простое обьяснение излучения Хокинга на основе моей новой идеи квантования поверхности черной дыры. Горизонт событий черной дыры является двухмерной поверхностью в форме сферы. Такую сферу рассматривают чисто как геометрический обьект, ее свойства аналогично мембране. Мембрана может колебаться, на ней возникают упругие волны.
Поэтому я подумал, что горизонт событий -это сферическая мембрана, обладающая упругими и волновыми свойсвами.Допустим на поверхности горизонта событий появляются упругие волны колебаний. Всякой волне можно сопоставить квант волнового поля.
Квант волны на поверхности горизонта событий черной дыры назовем буквой X.
Х-квант двигается по замкнутой сферической поверхности черной дыры. Волна Х-кванта накладывается сама на себя, разрешая определенные частоты колебаний.
 Условие квантования поверхности горизонта событий черной дыры такое же,
Условие квантования поверхности горизонта событий черной дыры такое же,
как квантование орбит Бора, потому что в обоих случаях дейсвуют один корпускулярно-волновой принципОно имеет вид:

(1)
Где
r- радиус черной дыры, n-квантовое число 1,2,....,N.
Частота и период колебаний волны Х-кванта на поверхности черной дыры определим по дисперсионной формуле:

(2)
Где с- скорость волны на поверхности горизонта событий равна скорости света, если предположить, что Х-квант безмассовый.
С другой стороны частота волны на поверхности связана с энергией Х - кванта по формуле Планка:
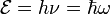
(3)
Получаем квантование энергии колебаний на поверхности черной дыры, если подставим все эти формулы (1,2,3):
Еn
= nhc/2 r
r (4)
Радиус горизонта r черной дыры зависит от ее массы r=2GM/с2, тогда формула (4) будет иметь следующий вид:

(5)
Получаем квантование энергетических уровней (5) колебаний поверхности черной дыры, в данной случае получается спектр линий, отстоящие друг от друга на величину:

(6)

При переходе из одного энергетического уровня m в другое состояние n поверхность горизонта событий черной дыры излучает фотон:
Emn= hv=Em - En
(6)
Такой процесс излучения горизонта событий черной дыры называется эффект Хокинга. Сам ученый пришел к такому выводу на основе анализа поляризации вакуума в сильном гравитационном поле вблизи поверхности черной дыры.
Я же показал, что этот эффект обусловлен квантованием поверхности горизонта событий, аналогично квантованию орбит по теории Бора.Теперь рассчитаем температуру поверхности, для этого средняя энергия фотона
при равновесном состоянии излучении определяется так:
E=hv=akT (7)
Где k- коэффициент Больцмана, T-температура, а-числовой коэффициент, зависящий от распределения теплового излучения светимость-частота.
С другой стороны энергия фотона определяется формулой (6), тогда используя формулу (7) получим температуру поверхности черной дыры:

(8)
Если коэффициент a

(при планковском распределении излучения), то получим формулу Хокинга для температуры поверхности черной дыры.
Можете сами провести анализ моей идеи, но в итоге получите эффект Хокинга для черной дыры.


