
— стороны четырехугольника,

— сумма длин его диагоналей. Докажите, что:
а)

;
б)
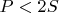
.
(ТурЛом,  )
)Доказываю:
Возьмём в ПДСК точки

и нарисуем четырёхугольник

.
Удвоенная сумма длин его диагоналей равна

, а периметр больше

.
Осталось лишь доказать, что

, но я сегодня целый день
(Оффтоп)
, поэтому туговато соображаю.
Пожалуйста, помогите решить.