Цитата:
Munin:
Да не вытекает из него (ур. КГ) парадоксов вообще. Уравнение как уравнение. Вытекают из него решения в разных гранусловиях, вот и всё.
...есть "парадокс Клейна" - в единственном числе, с именем, и в кавычках. А что вы произнесли:
Цитата:
Lvov в сообщении #739977 писал(а):
у меня недостаточно точное изложение парадоксов, вытекающих из уравнения К-Г.
- этого, повторяю, вообще в природе нет.
Судя по литературе, "парадокс Клейна" заключается в том, что определенное решение уравнения Дирака, описывающее прохождение электронной волны сквозь высокий заграждающий потенциальный барьер

, показывает, что при некоторой умеренной энергии частицы коэффициент ее прохождения равен 1, а коэффициент отражения равен 0. Это более "круто", чем те явления, о которых я говорил в своих сообщениях.
Я не рассчитывал коэффициент прохождения волны Клейна-Гордона через высокий заграждающий барьер, и поэтому говорил о недостаточно точном моем изложении вопроса. Однако легко показать, что и в случае УКГ при заграждающем барьере

существует такая умеренная энергия частицы

и соответствующий импульс

, при которых коэффициент прохождения частицы будет равен 1. И обратно, для любого умеренного значения импульса частицы (

), существует энергия заграждающего барьера

, при которой коэффициент прохождения частицы сквозь барьер равен единице.
Как я указывал в своем сообщении от 24.06.2013, 13:09 импульсы частицы перед и за барьером (

и

) удовлетворяет соотношениям

и

Приравняв значения указанных импульсов

, можно определить значение соответствующего заграждающего потенциала, которое в случае умеренного значения импульсов удовлетворяет соотношению

Пусть уравнения пространственных частей падающей, отраженной и проходящей волны имеют вид

Приравнивая амплитуды и первые производные суммы волновых функций слева и справа от барьера при

, получаем два уравнения для амплитудных коэффициентов рассматриваемых волн.


Решая указанную систему уравнений, получим
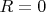
и

, т.е. коэффициент прохождения сквозь барьер волны равен 1, а коэффицент ее отражения равен 0.



