1)в частном случае рассмотрения -в задаче расчета волны в струне от начального импульса (импульса начальных скоростей ) возникает альтернатива как считать.
А)методом численного интегрирования
б)методом с подстановкой вычисленных аналитических значений интегралов.
Для стандартных прямоугольных и треугольных импульсов интегралы просты
Я-сторонник 2-го подхода
Проблема в том, что на самом деле существует не один, а несколько аналитических способов решения волнового уравнения. Вы познакомились пока только с одним.
Насколько я себе представляю, методы решения волновых уравнений примерно распадаются на три класса:
1. Методы характеристик и разделения переменных, представитель которых - решение Д'Аламбера.
2. Методы интегральных преобразований и разложения по собственным колебаниям, наиболее известен метод Фурье.
3. Методы обращения дифференциального оператора - фундаментальное решение и функция Грина.
Эти методы, кроме первого, применимы и к уравнениям неволнового типа, например, к параболическим и эллиптическим.
Метод Фурье в случае струны представлял бы собой разложение начального условия произвольной формы по гармоникам, и сложение их обратно в произвольный момент времени. Ваши рассуждения о стержне, по сути, апеллируют к этому методу. Уравнения с произвольным законом дисперсии удобно решать этим методом.
Метод функции Грина представляет собой вычисление колебания струны в случае начального условия специального вида - отклонения от нуля только в одной точке. После этого, это колебание интегрируется с тем начальным условием, которое реально дано. Первый шаг можно сделать для струны однократно, и потом интегрировать с многими разными начальными условиями.
-- 27.06.2013 17:27:07 --P. S. Частоту обозначают всё-таки не буквой
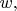
а похожей на неё греческой буквой "омега"

Такая ошибка "царапает глаз".



