========= 174 ========== ММ174 (А-4) (7 баллов)
Найти наименьшее натуральное число, произведение всех натуральных делителей которого заканчивается
а) ровно 2013 нулями;
б) не менее чем 2013 нулями.
Примечание:
Система счисления десятичная.
РешениеПриведу решение Алексея Извалова.
Безусловно это решение можно было бы изложить короче. Приводимый ниже текст - это, скорее, не результат, а процесс рассуждений Алексея.
Но...
Во-первых, весьма любопытно заглянуть "на кухню", где готовится решение, сопоставить чьи-то рассуждения со своими.
А во-вторых, некоторые из более коротких рассуждений привели рассуждавших к неверному ответу на вопрос пункта б)

Цитата:
Обозначим:

- само число,

- количество его делителей,

- количество нулей в конце этого числа.

- произведение всех

делителей числа

.
Если

, то у него будет

делителей. При этом, если число

оканчивается

нулями, то наименьшая из степеней двойки и пятерки должна равняться

(другая степень может и превосходить

).
(

)
Если число

имеет

делителей и

- чётно, то все делители числа

разбиваются на пары, дающие

в произведении. Тогда число

, произведение всех

делителей числа

будет равно

И если число

оканчивается на

нулей, то у данного произведения будет в конце

нулей.
Если же

- полный квадрат и у него нечётное количество делителей, произведение всех его делителей будет равно
![$n^{\left[\frac{k}{2}\right]}\sqrt{n}$ $n^{\left[\frac{k}{2}\right]}\sqrt{n}$](https://dxdy-03.korotkov.co.uk/f/a/b/e/abe64a0924e01518c35003e3e23089d582.png)
, т.е., опять-таки

имеющее

нулей в конце.
Поскольку как минимум один из множителей (2 или 5) входит в разложение числа

в степени

, а другой - как минимум в степени

, то

Если

оканчивается ровно 2013 нулями, то

Условию, связывающему

и

удовлетворяют следующие пары:


В первом случае минимальным будет число

Во втором:

Второй число меньше, так что оно и будет ответом на вопрос а)
Ответ:


Рассмотрим сначала число вида

.




Можем ли мы уменьшить искомое число? Число делителей удвоится, если

умножить на 3.
Тогда



Удвоим

снова, умножив

на 7.



Удвоим

снова, умножив

на 9 (увеличение выходит меньше, чем если бы умножить на 11).



Удваивать

, домножая на простые числа, будет выгодно, пока это позволит избавиться от двух нулей, а число. на которое домножаем, будет меньше 100.
Умножаем на 11:



Вот умножение на 13 приводит к неравенству



и число увеличилось.
Но необходим более систематичный подход для поиска минимального

. Который, к тому же, мог бы учитывать неравенство степеней двойки и пятёрки в числе

.
Понятно, что если двойка и пятёрка входят в разложение числа

не в равных степенях, то количество делителей не изменится, само число будет меньше, если степень двойки будет больше степени пятёрки.
Пусть

, где

, в разложение числа

не входят ни 2, ни 5, и число

имеет c делителей.
Тогда

А число

будет оканчиваться

нулями.


Для облегчения перебора, предварительно я построил таблицу минимальных чисел, не делящихся на 2 или 5 и имеющих ровно с делителей. (если числа нет в таблице, то оно больше миллиона. Как правило, это для простых c, когда минимальное

или для

)
2 3
3 9
4 21
5 81
6 63
7 729
8 189
9 441
10 567
11 59049
12 693
13 531441
14 5103
15 3969
16 2079
18 4851
20 6237
21 35721
22 413343
24 9009
25 194481
27 53361
28 56133
30 43659
32 27027
36 63063
40 81081
42 392931
45 480249
48 153153
54 693693
56 729729
60 567567
Для

,

Составим таблицу:
d c
0 9
1 8
2 8
3 7
.....
Увеличение

удваивает число, так что выгода в его увеличении будет лишь тогда, когда множитель В удаётся уменьшить более, чем вдвое.
Минимальное значение

будет достигаться при

,

При


Составим таблицу:
d c
0 14
1 12
2 11
3 10
4 9
5 8
.....
Минимум будет при

,

При


Составим таблицу:
d c
0 24
1 21
2 18
3 16
.....
Минимум будет при d=0, B=9009,

При
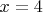

Составим таблицу:
d c
0 41
1 34
2 29
3 26
4 23
.....
Минимум будет при

(в таблице указано минимальное значение

, но для

значение

меньше, чем для

),

Дальнейшее уменьшение числа нулей в конце числа

приведёт к ещё большему росту числа

, который превысит выгоду от отказа от лишних множителей

.
На всякий случай я провёл перебор (со всеми оптимизациями) и получил, что действительно, наименьшее число, произведение всех делителей которого оканчивается не менее чем 2013ю нулями равно 900 900 000. Следующим будет 1 081 080 000
Ответ:
а)

б)

Сергей Половинкин нашел в Интернете задачу (предлагаемую в качестве образца задачи С6 ЕГЭ), где требовалось найти намиеньше натуральное число, произведение делителей которого заканчивается на 399 нулей.
Каюсь, одиннадцатиклассники, у которых я веду факультатив, приносили мне эту задачу (только не уверен, что там именно 399 нулей было). И именно она легла в основу ММ174.
Единственное существенное изменение - добавление пункта б), на мой взгляд, гораздо более содержательного, чем а). В частности, у меня ушло на второй пункт раз в 10 больше времени, чем на первый.
Поясню, как я оценивал решения. Одного балла недосчитались те участники, которые (хотя и упомянули, что решали пункт б) перебором) не привели ограничений, делающих перебор конечным.
Если же такие ограничения (пусть и не оптимальные) в решении были приведены, я ставил оценку 7 баллов. Но только при условии, что ответ верен

Сергей Половинкин (неожиданно для меня) нашел в условии скрытый намек на исследование задачи для других систем счисления. И прислал мне набросок такого обобщения.
Мне думается, что такое обобщение не вызывает особого интереса (в отличие, например, от ММ175). Поэтому дополнительных призовых баллов не было.
Что-то в текущем туре я стал жаден на дополнительные баллы. Но обещаю исправиться.
НаградыЗа решение задачи ММ174 Виктор Филимоненков, Алексей Извалов, Анатолий Казмерчук и Алексей Волошин получают по 7 призовых баллов. Сергей Половинкин и Олег Полубасов получают по 6 призовых баллов. Евгений Гужавин - 5 призовых баллов, а Николай Дерюгин - 4 призовых балла.
Эстетическая оценка задачи - 4.4 балла



