Что может помешать гравитационному полю изменяться во времени так, чтобы это можно было называть подходом сильной гравитационной волны к горизонту изнутри?
Уравнения Эйнштейна. Попробуйте найти решение, при котором «сильная» волна в пустом пространстве обгоняла бы свет.
Напомню, что речь, вообще-то, идёт о взаимодействии гравитационных волн. Но вы сначала почему-то попытались свести вопрос к выходу (одной) гравитационной волны из под (сферического) горизонта. А теперь вам почему-то нужна сверхсветовая скорость.
Всё это странно, но если уж вам так сильно нужна "сверхсветовуха", то я её вам дам...

Пусть есть пункт А и пункт Б. Расстояние АБ стопятьсот триллионов световых лет. Может ли гравитационная волна попасть из А в Б всего за одну секунду? Да, может, но нужен помощник - вспомогательная сильная гравитационная волна.
Гравитационные волны распространяются со скоростью света и являются поперечно-поперечными. Они в одном перпендикулярном распространению направлении пространство сжимают, а в другом растягивают.
Примерчик плоской гравитационной волны:
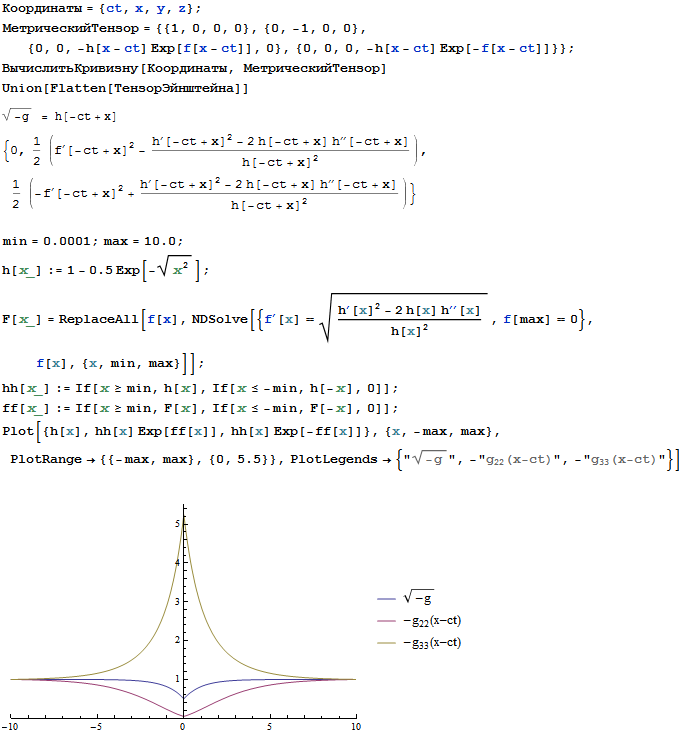
В этом примерчике гравитационная волна распространяется со скоростью света вдоль оси

. Расстояния вдоль оси

уменьшаются, а расстояния вдоль оси

увеличиваются. После того как волна проходит, расстояния вдоль осей

и

возвращаются в исходное состояние.
Так вот, в направлении перпендикулярном АБ пустим вспомогательную гравитационную волну, которая сократит расстояние между пунктами А и Б со стапятьсот триллионов световых лет до одной световой секунды. В это время исходная гравитационная волна распространяясь со скоростью света из пункта А прошмыгнёт в нункт Б за одну секунду. Потом вспомогательная гравитационная волна уйдёт и расстояние АБ опять станет стопятьсот триллионов световых лет.
Как видите, не смотря на то, что исходная и вспомогательная гравитационные волны распространялись со скоростью света, это не помешало исходной волне попасть из пункта А в пункт Б всего за одну секунду.
Теперь вернёмся к вопросу формирования чёрной дыры из нескольких сфокусированных гравитационных волн.
Не очевидно, что волны должны сколлапсировать в ЧД. Они могут как сойтись так и разойтись обратно. Формируемый гравитационный объект не обладает сферической симметрией.
Не очевидно, можно ли ему приписать какой-то конкретный "гравитационный радиус"

, а если вдруг и можно, то

будет зависеть от времени и может не только увеличиваться, но и уменьшаться за счёт излучения гравитационных волн.
Не очевидно, что

в конце концов стабилизируется на ненулевом значении.



