Да, верно. Голова вечером уже "не варила". Конечно, мое предложение надо читать наоборот
Тогда

- и не гравитационная масса. А снова
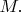
Поскольку "глупости надо подкреплять аргументами" , вот цитата из Вайнберга глава 11, пар. 9 , где он пишет про грав. коллапс.
Цитата:
Таким образом, жидкая сфера с начальной плотностью

и нулевым давлением переходит из состояния покоя в состояние коллапса с бесконечной плотностью собственной энергии за конечное время

Это к вопросу о бесконечной плотности.
Если почитать контекст, то будет ясно, в каком смысле эти слова тут произносятся. Если, конечно, стремиться думать мозгами, а не напротив, всеми силами избегать этого.
Конечно этого не может быть, поэтому я привел оценочный минимальный размер тела, когда оно полностью внутри горизонта. Это размер, когда действие ОТО кончается и она умывает руки.
Мне интересно, какую оценку минимального радиуса тела можете привести Вы или кто-то еще.
Вот только вместе с ОТО заканчивается и действие таких понятий, как "вещество", "масса" и "плотность". "Размер" не заканчивается, потому что его снаружи охватить можно. Так что, не в оценке радиуса дело.
А вот выражение для массы у Ландау (100.23) для произвольного случая , когда плотность может зависеть от времени:

Как видно интеграл берется по объему, как будто наш шар погружен в галилеево пространство. Это выражение справедливо только , если

, если меньше, то неправильно.
Вы не вычитали самого главного: в какой системе координат он берётся, и перестаёт существовать, если эта система координат теряет смысл, не может быть введена.
(Оффтоп)
scheknПо набору формул: штрих нельзя ставить в обратную сторону, как
` , тогда он не наберётся. Надо только в прямую:
' . Ещё вы до сих пор не научились ставить многобуквенные индексы: правильно пишется
g_{\mu\nu} , а не
g_\mu_\nu . И наконец, такие обозначения, как det, пишутся
\operatorname{det}или
\mathrm{det}\,- прямым шрифтом и с пробелом
\, , чтобы не сливались в одно слово. Для некоторых таких обозначений есть даже отдельные команды: \ln . И наконец, дифференциалы тоже стоит отбивать пробелами, чтобы не сливались:
a\,dv\,dr\,r даёт удобочитаемый результат:

(Оффтоп)
Кстати, зря вы пеняете, что "учитель плох". Я посмотрел, в сентябре прошлого года - полгода назад - вы путались в гораздо более элементарных вещах. То есть за полгода прогресс есть, и очень существенный, я ему рад. Вот только ему мешает ваша бессистемность: вы хватаетесь сразу за то, что не можете прожевать, и не движетесь к нему постепенно по последовательно связанным темам. И видимо, у вас просто настроение такое - всё время ругать тех, кто щедро тратит своё время и силы, чтобы вам помогать, хаять учебники, воротить нос от хорошего, и даже когда оно оказалось для вас хорошим - всё равно не выдавливать из себя ни слова высокой оценки и благодарности.
-- 19.03.2013 14:34:31 --Можно для начала рассмотреть задачку попроще. Пусть есть готовенькая чёрная дыра. На неё падает гравитационная волна. Гравитационная волна сгинет внутри или же прошибёт дыру насквозь и выйдет с противоположной стороны?

От длины волны зависит. Вообще, есть книжка такая:
Новиков И.Д., Фролов В.П. Физика чёрных дыр (Наука, 1986)
в ней много чего полезного написано.