Someone писал(а):
Не понял, какое отношение данное изменение условий ВТФ, делающее её неверной, имеет к теореме Пифагора?
Уравнение

стало бы частным случаем ТФ и доказать, что оно имеет решение в целых числах было бы также трудно, как и ТФ.
Someone писал(а):
Бесконечномерные векторы над полем рациональных чисел.
Впервые получаю такой ответ. Только почему они бесконечномерные?
А рациональные числа - не векторы?
§22. Первая трехмерная модель чисел.
Трехмерные модели чисел получаться из формулы (17), когда равны нулю все коэффициенты при единичных векторах, кроме каких либо трех. Основные из этих моделей могут иметь вид:

Очевидно, здесь также, модели, определяемые тремя одноименными буквами, будут относиться к редко используемым, а потому мы их здесь не выписываем. Кроме этих канонических моделей, трехмерные модели чисел могут иметь неканонический вид, например:

При

и

отличных от нуля, опуская индексы, получим из формулы (17):

Каноническую модель чисел, которую будем изображать в трехмерном пространстве с действительной осью

и двумя меточными осями

и

вектором, исходящим из начала координат и концом в точке

. Эту модель мы будем называть основной или первой трехмерной моделью. Она может принимать неканонический вид

В определении (28)

– действительные модели чисел,

– единичные меточные векторы; при этом для трехмерных моделей

и

введены понятия равенства, арифметические и векторные операции по следующим правилам:
1)

тогда и только тогда, когда

и

.
2)

.
3)

.
4)

,
где

.
5)

, или

.
6)
![$$
[w_1w_2] = \begin{vmatrix}
1 & i & j\\
x_1& y_1 & z_1 \\
x_2& y_2 & z_2
\end{vmatrix}
$$ $$
[w_1w_2] = \begin{vmatrix}
1 & i & j\\
x_1& y_1 & z_1 \\
x_2& y_2 & z_2
\end{vmatrix}
$$](https://dxdy-02.korotkov.co.uk/f/1/4/b/14be7ed3126ac91cd842d472074f1ccc82.png)
.
При этом
![$ [1i] = -[i1] = j, [ij] = -[ji] = 1, [j1] = -[1j] = i $ $ [1i] = -[i1] = j, [ij] = -[ji] = 1, [j1] = -[1j] = i $](https://dxdy-01.korotkov.co.uk/f/0/a/e/0ae747deb59df5b309d72c69ccde1c0882.png)
, ,.
7)

где

Из 1) и 3) следует, что меточные единичные векторы удовлетворяют формулам (28). Из 3) и 4) заключаем, что операции умножения, и деления трехмерных моделей нарушают их каноническую форму.
Таким образом, введенные операции сложения и умножения обладают свойствами коммутативности

,
Ассоциативности

и дистрибутивности

Из свойств 1) следует, что множество трехмерных моделей чисел содержит в себе, как часть множество всех одномерных моделей чисел

и

, а также множество всех рассмотренных выше двумерных моделей чисел.
Операция деления осуществляется на основе определения единичных меточных векторов. Сначала, осуществляется перевод знаменателя к неканоническому вектору

, (уничтожаются векторы

и

путем умножения знаменателя и числителя на трехмерную модель)

.
Вторым умножением числителя и знаменателя на модель, сопряженную (относительно вектора

знаменателю уничтожается вектор

.
Операцию деления можно определить, как операцию, обратную операции умножения. Пусть, при

, имеем

Тогда

Подставляя сюда выражения

, и

, получим

Производя умножение, получим, приравнивая коэффициенты при соответствующих единичных векторах систему линейных уравнений для определения неизвестных

и
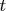
.

Определитель системы

следовательно, система имеет единственное решение. Числители неизвестных, также, совпадут с соответствующими числителями, приведенными в пункте 6). При практических вычислениях, лучше применять первый метод деления трехмерных моделей.
Пример. Пусть

, тогда


;

;
![$$
[w_1w_2] = \begin{vmatrix}
1 & i_1 & j\\
2 & 1 & -3 \\
1 & -4 & 5
\end{vmatrix} = - 7 - 13i - 9j
$$ $$
[w_1w_2] = \begin{vmatrix}
1 & i_1 & j\\
2 & 1 & -3 \\
1 & -4 & 5
\end{vmatrix} = - 7 - 13i - 9j
$$](https://dxdy-04.korotkov.co.uk/f/3/5/7/3572884951d1303c4a3a976109ceb28c82.png)
;

Скалярная величина

.
называется модулем трехмерной модели или длиной вектора

. Если

и

- углы, образуемые вектором

соответственно с осями

и

, то

.
Подставляя эти выражения в соотношение (29), получим тригонометрическую форму трехмерной модели

.



