Элементарных доказательств ВТФ нет и не может быть

[Someone]

Yarkin писал(а):

Это не мною выдумана природа числа. Определение дано Пифагором. Каким образом за последнее тысячелетие оно потеряло материальность?

Начхать на то, что думал Пифагор о природе числа. У Пифагора не было современного понятия числа. Его не было и гораздо позже, например, у Архимеда. И математика с того времени очень далеко ушла и от Пифагора, и от Архимеда.

Yarkin писал(а):

У математиков таким материалом должны быть абстрактные модели, среди которых могут быть как плохие, так и хорошие. Аппаратом по обработке будут операции с моделями. Модель и операции можно выбирать, усложнять или упрощать

В общем-то, примерно так и есть, но Ваши представления в высшей степени наивны - вследствие малого знания математики.

[Yarkin]

Brukvalub писал(а):

Теперь мне от Вас нужно еще одно усилие: что нового в математике или ее приложениях позволяют понять или получить Ваши модели чисел, кроме самих моделей? Без появления таких примеров считаю дальнейшее обсуждение моделей таким же бессмысленным, как и введение в календарь новой даты: 42 мартабря

Любое действие над моделью будет связано с природой. Вместо противоречивой системы (см. табл. 1), мы получим непротиворечивую (см. табл. 2), а для ВТФ мы получим рис. 1.
А из рис. Следует несостоятельность ТФ и всех имеющихся доказательств.

tolstopuz писал(а):

Я знаю определение квадратного уравнения и определение корня уравнения. А в каком определении написано, что квадратное уравнение имеет четыре корня?

По определению корня – четыре. Нигде. Теория не может учесть все. Возникающие противоречия надо исследовать. Но проще это объяснить незнанием автора.

tolstopuz писал(а):

А я уравнение называю уравнением, а корни - корнями. Во избежание путаницы.

Решение, которое мы выписываем, должно иметь одинаковую структуру.

Добавлено спустя 11 минут 2 секунды:

Someone писал(а):

Начхать на то, что думал Пифагор о природе числа. У Пифагора не было современного понятия числа. Его не было и гораздо позже, например, у Архимеда. И математика с того времени очень далеко ушла и от Пифагора, и от Архимеда

Теорема Пифагора звучала бы также, как и ТФ и ее не могли бы доказать!

Someone писал(а):

В общем-то, примерно так и есть, но Ваши представления в высшей степени наивны - вследствие малого знания математики.

Спасибо и за это.

[Brukvalub]

Yarkin писал(а):

Brukvalub писал(а):

Теперь мне от Вас нужно еще одно усилие: что нового в математике или ее приложениях позволяют понять или получить Ваши модели чисел, кроме самих моделей? Без появления таких примеров считаю дальнейшее обсуждение моделей таким же бессмысленным, как и введение в календарь новой даты: 42 мартабря

Любое действие над моделью будет связано с природой. Вместо противоречивой системы (см. табл. 1), мы получим непротиворечивую (см. табл. 2), а для ВТФ мы получим рис. 1.
А из рис. Следует несостоятельность ТФ и всех имеющихся доказательств.

Получается, что своей моделью Вы не вкладываете еще один кирпич в стройное здание математики, а рушите его, но не за ради чего-то, а во имя торжества Вашей нелепой модели. Лет 15 назад я смотрел фильм Т. Абуладзе "Покаяние" (см. http://www.krugosvet.ru/articles/66/100 ... 6658a1.htm), так в нем одна старая женщина совершенно справедливо вопрошала: "зачем нужна дорога, которая не ведет к храму?" Вот и Вам я советую ответить себе самому на этот вопрос.

[bot]

Yarkin писал(а):

tolstopuz писал(а):
Я знаю определение квадратного уравнения и определение корня уравнения. А в каком определении написано, что квадратное уравнение имеет четыре корня?
По определению корня – четыре.

Вот как, уже четыре? Всегда? Между прочим, при редактировании в этом утверждении я перенёс слово действительное в другое место и получилось неверное утверждение.
Его следует исправить так:
В Вашей алгебре всякое квадратное уравнение с действительными коэффициентами (или с любыми, но с обратимым старшим коэффициентом) и отличным от нуля дискриминантом имеет 4 корня.
Обобщение на случай произвольных коэффициентов неверно - корней может не быть вообще, может быть 4, а может быть и бесконечно много.
Если использовать матричное представление (в кольце матриц 4 на 4), то сразу обнаруживаются вырожденные матрицы, что неудивительно из-за присутствия делителей нуля. А это означает, что в Вашей алгебре даже линейное уравнение может как не иметь корней, так и иметь их бесконечно много.
Вот простые примеры:
$(j+1)x-1=0, \ \ (j+1)x-j-1=0$
Первое не имеет корней, а во втором их бесконечно много.

На Ваш вопрос о "скалярности" или "векторности" числа, а также на Ваши "обобщения" теоремы косинусов, признаюсь честно, по собственной инициативе отвечать не хотелось, письмо из канцелярии доставили прямо мне, минуя вышестоящее начальство, а потому на нём не оказалось обязывающей резолюции.
Однако где-то в начале этой ветки я давал косвенный ответ. Всё зависит от контекста, в котором это рассматривается. Например, если мы рассмотрим произвольное поле, как векторное пространство над самим собой (или над своим подполем), то один и тот же объект может рассматриваться и как число и как вектор, и тут уже дело пишущего - различать их с помощью обозначений или оставить читателю улавливать эти различия из контекста. Важно не то, как назвать объект, важно определить, что с ним можно делать - хоть горшком назови ...

Yarkin писал(а):

bot писал(а):
Ну тогда остаётся только одно - это я перепутал запах с цветами.

Там, откуда Вы взяли мою цитату о полноте, речь шла о двух моделях. Вы привели вид трехмерной и четырехмерной моделей. Для них она будет полной.

Никакого вида я не приводил.
Все вкладывают один и тот же смысл в замкнутость операции на множестве и полную определённость операции на множестве - в данном случае произведение: для всяких элементов a и b, принадлежащих M, существует элемент c из M, такой что ab=c.
Размерность линейной оболочки, натянутой на 1,i,j действительно 3, элемент k ей не принадлежит и стало быть элементы этой оболочки не составляют алгебру, так как она не замкнута относительно умножения или, что то же самое операция умножения на ней определена лишь частично, то есть не является полной. О полноте (в этом смысле) можно говорить только в случае, если рассматривать линейную оболочку 4-х элементов 1, i, j, k.

[Yarkin]

Brukvalub писал(а):

Получается, что своей моделью Вы не вкладываете еще один кирпич в стройное здание математики, а рушите его, но не за ради чего-то, а во имя торжества Вашей нелепой модели.

Я достаточно имел дело с кирпичами, строя свой дом, но никогда не разрушал "стройное здание" и не буду. "Нелепые модели" помогают раскрыть физический смысл наших абстрактных действий с ними.

bot писал(а):

Вот простые примеры:

Первое не имеет корней, а во втором их бесконечно много.

Насчет первого согласен, а второе имеет единственный корень 1. Но и в нашей математике есть такие уравнения.

bot писал(а):

Однако где-то в начале этой ветки я давал косвенный ответ. Всё зависит от контекста, в котором это рассматривается. Например, если мы рассмотрим произвольное поле, как векторное пространство над самим собой (или над своим подполем), то один и тот же объект может рассматриваться и как число и как вектор, и тут уже дело пишущего - различать их с помощью обозначений или оставить читателю улавливать эти различия из контекста. Важно не то, как назвать объект, важно определить, что с ним можно делать - хоть горшком назови ...

Значит я не должен искать разности между скаляром и вектором?
Корни уравнения могут быть и скалярами и векторами?[
quote="bot"]
О полноте (в этом смысле) можно говорить только в случае, если рассматривать линейную оболочку 4-х элементов 1, i, j, k.[/quote]
Именно это я имел в виду.

[Someone]

Yarkin писал(а):

Someone писал(а):

Начхать на то, что думал Пифагор о природе числа. У Пифагора не было современного понятия числа. Его не было и гораздо позже, например, у Архимеда. И математика с того времени очень далеко ушла и от Пифагора, и от Архимеда

Теорема Пифагора звучала бы также, как и ТФ и ее не могли бы доказать!

Это почему же она звучала бы так же, как теорема Ферма, и почему её не могли бы доказать?

bot писал(а):

А это означает, что в Вашей алгебре даже линейное уравнение может как не иметь корней, так и иметь их бесконечно много.
Вот простые примеры:
$(j+1)x-1=0, \ \ (j+1)x-j-1=0$
Первое не имеет корней, а во втором их бесконечно много.

Yarkin писал(а):

Насчет первого согласен, а второе имеет единственный корень 1.

Подсказка: $j$ также является корнем второго уравнения. Найдите ещё корни.

[Yarkin]

Someone писал(а):

Это почему же она звучала бы так же, как теорема Ферма, и почему её не могли бы доказать?

Потому, что там не было бы аргумента.

Someone писал(а):

Подсказка: также является корнем второго уравнения. Найдите ещё корни.

Теперь понятно! 2-j.






§20. Третья двумерная модель чисел.

Полагая в формуле (17) $ \eta = 2, x = 0, y_2 = y, z_2 = z, i_2 = i, j_2 = j $, получим

$$ w = iy + jz \eqno (24) $$

_ третью двумерную модель чисел. Здесь $ y $ и $ z $ – действительные модели чисел, $ i $ и $ j $ –единичные векторы, определяемые по формулам (11) и (12). Для двух векторов $ w_1=iy_1 + jz_1 $ и $ w_2 = iy_2 + jz_2 $ введены понятия равенства, арифметические и векторные операции по следующим правилам:
1) $ w_1 = w_2 $ тогда и только тогда, когда $ y_1 = y_2 $ и $ z_1 = z_2; iy + 0j = iy, 0 + jz = jz, 1i = i, 1j = j $.
2) $ w_1 \pm w_2 = i(y_1 \pm y_2) + j(z_1 \pm z_2) $.
3) $ w_1w_2 = z_1z_2 – y_1y_2 +k(y_1z_2 + z_1y_2) $.
4) $ \frac{w_1}{w_2} = \frac{y_1y_2 + z_1z_2}{y^2_2 +z^2_2} + k \frac{y_1z_2 - y_2z_1}{y^2_2 + z^2_2}, y^2_2 + z^2_2 \ne 0 $.
5) $ (w_1w_2) = |w_1||w_2|\cos\varphi $.
6)

$$ [w_1w_2] = \begin{vmatrix} i & j & k_{ij}\\ x_1& y_1 & 0 \\ x_2& y_2 & 0 \end{vmatrix} $$

где $ k_{ij}=[ij]=-[ji] $ - единичный вектор, перпендикулярный плоскости векторов $ i $ и $ j $, где единичный (канонический) вектор $ k $ определяется по формуле (13), $ \varphi $ - угол между векторами $ w_1 $ и $ w_2 $,
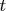
Таким образом, введенные операции сложения и умножения обладают свойствами коммутативности, ассоциативности и дистрибутивности. Из 3) и 4) усматриваем, что операции умножения и деления переводят эту модель из рассматриваемой плоскости в новую, (не каноническую, модель числа) с действительной осью $ x $ и мнимой осью $ t $ с единичным вектором $ k $.
Из свойств $ iy+0 = iy, 0 + jz = jz $ следует, что множество введенных двумерных моделей чисел, содержит в себе, как часть, множества вторых и третьих одномерных моделей чисел, а потому эта модель является для них расширением.
Вектор $ \bar{w} = jz - iy $ называется сопряженным к вектору $ w = jz + iy $. Значение $ |w| = \sqrt(y^2 + z^2) $ называется модулем вектора $ w $. На этой плоскости также можно ввести полярные координаты $ (\rho; \varphi): z = \rho\cos\vazrphi, y = \rho\sin\varphi (|w| > 0) $, получим, подставляя в (24)

$$ w = \rho(J\cos\varphi + i\sin\varphi), \eqno (25) $$

По определению положим

$$ e^{k\varphi} = \cos\varphi + k\sin\varphi, \eqno (26) $$

тогда, соотношение (25) можно представить в виде

$$ wj = \rho(\cos\varphi + k\sin\varphi) $$

в так называемой, тригонометрической форме. Учитывая свойства мнимых единичных векторов $ i $ и $ j $, от тригонометрической формы можно перейти к показательной:

$$ wj = \rho e^{k\varphi} $$

§21. Четвертая двумерная модель чисел.

Эта модель получается из первой двумерной модели простой заменой единичного вектора $ i $ на единичный вектор $ k $ и имеет вид

$$ w = x + ku $$

Поскольку значения степеней этих двух векторов совпадают, то все результаты, имеющиеся для первой двумерной модели, автоматически переносятся на эту модель. Фактически эти две модели являются параллельными, но имеющими различные связи с другими моделями. Рассматриваемая модель числа, в отличии от первой, является неканонической.

[bot]

Yarkin писал(а):

Someone писал(а):

Это почему же она звучала бы так же, как теорема Ферма, и почему её не могли бы доказать?

Потому, что там не было бы аргумента.

Угол ему в теорему Ферма подавай!

Yarkin писал(а):

Теперь понятно! 2-j.

Что Вам понятно в Ваших (а не в наших) "моделях"? Сказано ведь было, что корней бесконечно много. Причина этой бесконечности называлась, может быть Вам её растолковатьт?

Yarkin писал(а):

Значит я не должен искать разности между скаляром и вектором? Корни уравнения могут быть и скалярами и векторами?

bot писал(а):

О полноте (в этом смысле) можно говорить только в случае, если рассматривать линейную оболочку 4-х элементов 1, i, j, k.

Именно это я имел в виду.

Трудно представить, что Вы имеете в виду, если пишете прямо противоположное:
Вы рассматривали "модели" вида $a+bi+cj$ и утверждали, что их множество замкнуто относительно умножения.
Как Вы вообще понимаете эти линейные комбинации?
Я спрашивал, а Вы не ответили - представимо ли произвольное действительное число в виде $a+bi+cj$?
Я бы не стал задавать этот глупый на первый взгляд вопрос, однако это Вы меня вынуждаете к этому своими представлениями о действительных числах, согласно которым следует различать сущности и запахи, такие как $(+1)\cdot a$ и $a$.
Прежде чем строить расширение множества действительных чисел (или их понятия - кто же знает, что у Вас на уме?) не лучше ли с них и начать? А иначе опять Вы будете писать одно, а подразумевать то, о чём никто не догадывается.

[Someone]

Yarkin писал(а):

Someone писал(а):

Это почему же она звучала бы так же, как теорема Ферма, и почему её не могли бы доказать?

Потому, что там не было бы аргумента.

Какого аргумента?

[bot]

Someone писал(а):

Какого аргумента?

Да я уже расшифровал - встречался уже потому что.

Угол ему в теорему Ферма подавай, иначе он её бессмысленной считает!

И-эх, оно того стоит, чтобы процитировать без купюр его шедевр о двух ошибках
математиков, предавших Пифагора:

P.S. Что то восстаёт против цитирования.
Попробую отдельно.

[Someone]

Yarkin писал(а):

Someone писал(а):

Начхать на то, что думал Пифагор о природе числа. У Пифагора не было современного понятия числа. Его не было и гораздо позже, например, у Архимеда. И математика с того времени очень далеко ушла и от Пифагора, и от Архимеда

Теорема Пифагора звучала бы также, как и ТФ и ее не могли бы доказать!

Я всё-таки и после разъяснетий botа не понимаю. Стандартно теорема Пифагора формулируется так: Сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы. Или, эквивалентно: Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.

Чем тут современное понятие числа мешает? Как, по Вашему мнению, должна формулироваться теорема Пифагора при современном понимании числа? И чем тут помогут Ваши "модели", в которых Вы и сами никак разобраться не можете?

И ещё раз рекомендую почитать для начала хотя бы книгу А.Г.Куроша - параграф о линейных алгебрах плюс то, что Вам потребуется для понимания этого параграфа. То, что Вы пытаетесь строить - это и есть линейные алгебры.

[bot]

Теорема Пифагора (обобщенная). В прямоугольном треугольнике с прямым углом
$n\varphi = \frac{\pi}{2}$, катетами с длинами $\rho_1, \ \rho_2$
и гипотенузой с длиной $\rho$ имеет место равенство

$\rho_1^{2n} + \rho_2^{2n} = \rho^{2n}, \ \ n=1, 2, ... \ \ \ \ \ \ \ \ \ (1)$

Добавлено спустя 35 секунд:

Теорема может быть обобщена на произвольное значение $n$, ибо
$\pi$ - иррациональное значение, более того $n$ и $\varphi$ могут быть либо оба отрицательны, либо оба положительны.
При $n=1$ получается обычная ТП.

Добавлено спустя 5 минут 51 секунду:

Глубокий смысл обобщённой ТП в том, что она определяет допустимые операции над
величинами $\rho_1, \ \rho_2, $ в зависимости от значения $n$.
Так при $n=1$ мы должны складывать их квадраты, а при
$n=\frac{3}{2} $ - их кубы и т.д. И обратно. Если мы сложили их, то это означает,
что $n=\frac{1}{2} $,

Добавлено спустя 5 минут 13 секунд:

а если сложили их квадраты, то должно быть $n=1$ и т.д.
Мы подошли к первой ошибке. Сравните эту теорему с "Великой теоремой Ферма" (ТФ).
У ТФ, в отличие от обобщенной ТП нет угла и никакого права действия с тройкой $x, y, z $
- целыми или нет, участвующих в соотношении

Добавлено спустя 2 минуты 23 секунды:

$x^n + y^n = z^n, \ \ \ \ \ \ (2)$

мы не имеем . Но если предположить, что мы эти действия осуществляем, то давайте сюда
угол. С углом доказательство соотношения (2) для целых $x, y, z$ носит
элементарный характер. Следовательно ТФ доказывать не следует, ибо она сформулирована с ошибкой.

Добавлено спустя 9 минут 40 секунд:

P.S. Всего пара латеховских ошибок плюс ужасная связь, а также, видимо, не без этого:

Цитата:

Сообщения: 666

привели к совершенно зверскому расчленению цитаты.
Тут уже не до форматирования, но ни одной буквы в цитате не изменил.

[Someone]

bot писал(а):

И-эх, оно того стоит, чтобы процитировать без купюр его шедевр о двух ошибках математиков, предавших Пифагора:

Цитата:

http://www.zerkalo21.uz/eto_interesno/dokazana_li_velikaya_teorema_ferma.mgr
Такую ошибку содержит и современное понятие числа. Оказывается, что оно в корне отличается от его древнего представления, сформировавшегося естественно-историческим путем. Чтобы убедиться в этом, достаточно вспомнить определение числа, данное Пифагором. По Пифагору, число – материальный объект, а по нашему представлению - это скаляр и не определяемое первичное понятие. Разница существенная.
Создавая аксиоматику натуральных чисел, Пеано и его последователи считали, что они знают, что такое число. Увы, они простейшее изображение числа приняли за число!

Это?

[Yarkin]

Да

Добавлено спустя 23 минуты 22 секунды:

Someone писал(а):

Я всё-таки и после разъяснетий botа не понимаю. Стандартно теорема Пифагора формулируется так: Сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы. Или, эквивалентно: Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.

Достаточно взять формулировку ТФ и заменить требование $ n > 2 $ на $ n > 1$.
K Вам у меня тот же вопрос: ействительные числа векторы или скаляры. bot ответил "горшками", а Вы?

[Someone]

Yarkin писал(а):

Someone писал(а):

Я всё-таки и после разъяснетий botа не понимаю. Стандартно теорема Пифагора формулируется так: Сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы. Или, эквивалентно: Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.

Достаточно взять формулировку ТФ и заменить требование $ n > 2 $ на $ n > 1$.

Не понял, какое отношение данное изменение условий ВТФ, делающее её неверной, имеет к теореме Пифагора?

Someone писал(а):

K Вам у меня тот же вопрос: ействительные числа векторы или скаляры. bot ответил "горшками", а Вы?

Бесконечномерные векторы над полем рациональных чисел.