Уравнение приводим к виду

. Для уравнения

известно общее решение в натуральных числах

, где

взаимно простые.
А имено

, где

- натуральные числа,

и
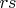
- четное число.
У нас

, следовательно,

, откуда

.
Легко показать, что эта дробь не может быть целым числом (не то что целым квадратом), исключая

.
А поскольку при отрицательных

правая часть исходного уравнения меньше нуля, то других решений кроме

нет.
Остается посмотреть что будет при

. Нет никаких решений.
Замечу, что на исходной эллиптической кривой бесконечно много рациональных точек, порожденных одной точкой

, поскольку ранг кривой единица. Рациональных точек конечного порядка на кривой нет (кроме

).



