Пытаюсь разобраться с релятивистской квантовой теорией. Под релятивистской понимается как кванты в СТО, так и в ОТО.
Буду благодарен, если кто-нибудь поможет с литературой по данной тематике? Особенно интересуют книги для которых справедливо как минимум одно из утверждений:
1)Написана позднее 1980 года
2)Используются в основном обозначения Дирака
3)Содержит хоть сколько-нибудь разобранные примеры
Так же буду благодарен, если поможете с литературой, где спин разбирается больше с математической точки зрения.
Так же есть несколько вопросов по релятивистским квантам:
1) В той литературе, которая мне попадалась, функция Гамильтона вводилась как

, где

- лагранжиан,

- полевые переменные,

- сопряженные им импульсные переменные.
Но такой подход не очень-то релятивистски инвариантен, потому что время выделяется явно.
Это можно исправить, если определить Гамильтониан как

. При этом получаются и скобки Пуассона и уравнения Гамильтона.
Делал ли кто-нибудь что-то подобное, и если делал то где?
2) Правильно ли я понимаю, что для описания не релятивистского спина волновую функцию заменяют с "обычной" комплексной функции на комплексную функцию умноженную на матрицу

и спин начинает описываться элементами пространства
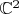
. При этом строят гомоморфизм группы вращения пространства в группу вращений спинового пространства
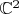
.
И как при этом строят релятивистский спин?



