Докажите, что Вася где-то ошибся.
Ранг великоват, ч.т.д.
Н3. Для комплексного

, удовлетворяющего неравенству

, определите наименьшее и наибольшее значение выражения

.
Очевидно, что
![$|z^2-5|\in[5-|z|^2;\,5+|z|^2]\subset[5-2^2;\,5+2^2]=[1;9],$ $|z^2-5|\in[5-|z|^2;\,5+|z|^2]\subset[5-2^2;\,5+2^2]=[1;9],$](https://dxdy-02.korotkov.co.uk/f/1/1/2/112609c2b48bf2263973ce1c1b70039b82.png)
причём верхняя граница достигается на

и нижняя -- на
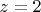
.
Что-то как-то неолимпиадно. Следующее тоже вполне шаблонно:
Н2. Определить все действительные значения параметра

, при каждом из которых уравнение

имеет три различных действительных корня.
Чтобы был кратный корень, надо, чтобы в нём обращалась в ноль не только сама функция, но и её производная:

(равносильно, т.к. заведомо

). Из соображений монотонности следует, что областью существования трёх вещественных корней будет

.
-- Вс окт 28, 2012 19:02:08 --"Это" равносильно

, что легко доказывается по индукции.
Не, не надо индукции: если разделить исходную дробь почленно, то стремление последней дроби к единице тривиально, предпоследней к нулю -- тоже, а каждая из предыдущих меньше, чем

, и при этом их количество меньше, чем

.