========= 165 ========== ММ165 (РК-5) (7 баллов)
По мотивам задачи ММ74 Вася и Петя поспорили.
Вася утверждает, что объем выпуклого многогранника, все грани которого правильные многоугольники, а все 15 ребер имеют длину 1 заведомо больше объема каждого из выпуклых многогранников, о которых идет речь в задаче ММ74. Петя же утверждает, что не больше, а меньше.
В качестве третейского судьи позвали Федю. Подумав, Федя пришел к выводу, что возможны разные типы выпуклых многогранников с 15-ю единичными ребрами, все грани которых - правильные многогранники. Для одних объем, заведомо больше объема любого из многогранников из ММ74, а для других - наоборот меньше.
Кто прав?
РешениеОбъемы многогранников из задачи ММ74 равны соответственно
![$\frac{2+\sqrt 2}{3 \sqrt[4]2}\approx 0.957$ $\frac{2+\sqrt 2}{3 \sqrt[4]2}\approx 0.957$](https://dxdy-04.korotkov.co.uk/f/3/6/5/365a06408af9f57b81ba395741ada77d82.png)
(антипризма) и

("домик").
Объем правильной пятиугольной призмы, боковая грань которой - квадрат со стороной 1, примерно равен

, поэтому Петя не прав.
Объем правильной пятиугольной бипирамиды, боковая грань которой - правильный треугольник со стороной 1, равен примерно

, поэтому Вася тоже не прав.
На этой стадии мы можем констатировать, что Федя прав. Тем участникам, кто не согласен с таким выводом (а, судя по присланным решениям, их большинство), рекомендую еще раз прочитать утверждение Феди.
ОбсуждениеЗадача содержала ловушку, в которую угодили даже опытные марафонцы. Естественным образом возникает вопрос: не существует ли подходящего многогранника, объем которого больше объема антипризмы, но меньше объема "домика". Оказывается, такой многогранник существует. А то, что его существование не противоречит утверждению Феди, отходит на второй план.
Выясним, какие же еще выпуклые многогранники можно составить из 15-и единичных ребер так, чтобы все грани были правильными многоугольниками.
Кроме, пятиугольной бипирамиды существует еще один "Петин" многогранник. Это правильная треугольная призма с квадратными боковыми гранями, к основаниям которой пристроены правильные тетраэдры. Ее объем равен примерно

.
Наибольший интерес представляют два многогранника.
О существовании первого (он называется "triangular cupola") не догадываются Вася и Петя, а возможно и Федя.
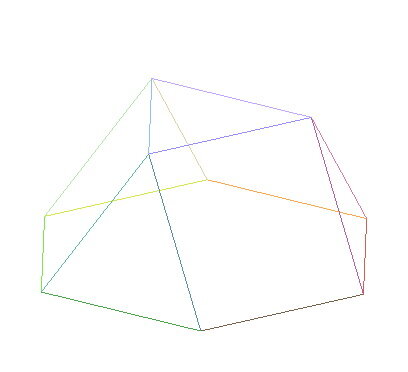
Его нашли Сергей Половинкин, Олег Полубасов, Виктор Филимоненков и Николай Дерюгин.
Для его описания и простого нахождения объема возьмем куб со стороной

и разрежем пополам сечением, проходящим через центр диагонали перпендикулярно к ней. Объем одной части, очевидно, равен

.
Нижним основанием нашего многогранника возьмем шестиугольник, получивший в сечении. В качестве вершин верхнего основания возьмем середины уцелевших при рассечении куба ребер.
Теперь для получения нашего многогранника осталось только отсечь четыре уголка бывшего куба. Объем каждого, очевидно, равен

.
Окончательно объем нашего многогранника равен

, т.е больше, чем у четырехугольной антипризмы, и меньше, чем у "домика".
Еще один подходящий многогранник (он называется "Tridiminished icosahedron") обнаружили Анатолий Казмерчук и Николай Дерюгин. (Но не Петя. Знакомы ли с ним Вася с Федей - неизвестно.)

Этот многогранник можно получить из правильной пирамиды с ребром основания 2 и высотой

.
Для этого надо отрезать верхушку пирамиды (по средним линиям боковых граней) и три тетраэдра у оснований (сечения нужно проводить через середины ребер основания и точки на боковых ребрах, удаленные от этих середин на 1).
Непосредственно проверяется, что все грани оставшегося многогранника - правильные многоугольники со стороной 1.
Объем этого многогранника примерно равен

(у Анатолия Казмерчука при совпавших промежуточных результатах почему-то получилось

).
Как сказано в комментариях к задаче ММ74, существует ровно 92 джонсоновых многогранника (джонсоновыми называются выпуклые многогранники, отличные призм, антипризм, платоновых и архимедовых тел, у которых все грани правильные многоугольники).
Четыре из них имеют по 15 ребер. Вместе с пятиугольной призмой они дают все подходящие многогранники.
В частности, не годится еще один многогранник, "найденный" некоторыми марафонцами (в ряды которых затесался, было, и ведущий): Это правильные октаэдр и тетраэдр, склеенные по грани.
Прикинув "на глазок", я решил, что такая комбинация дает выпуклый многогранник. В принципе так и оказалось...
Только вот один из углов между гранями получается развернутым. Поэтому две треугольные грани сливаются в одну, имеющую форму ромба. К тому же, ребер остается всего 14, так как одно превращается в диагональ грани.
Не годится (просто не проходит по числу ребер) и "верхушка ромбокубооктаэдра", предложенная одним из участников.
Расскажу о том, как возникла задача.
Сначала я обнаружил triangular cupola и увидел, что его объем, в отличие от объемов "очевидных" многогранников, находится между объемами многогранников из ММ74.
Я решил обыграть это обстоятельство и ввел Федю, который по замыслу тоже должен был ошибиться. Но никак не мог нормально сформулировать соответствующее утверждение Феди. После очередного "все выпуклые многогранники, имеющие по 15 ребер, длина каждого из которых равна 1, и такие, что каждая грань является правильным многоугольником, можно разбить на два класса так, что объем любого многогранника из первого класса меньше объема каждого из многогранников, о которых говорится в задаче ММ74, а объем любого многогранника из другого класса...", я плюнул, решил, что Федя не Дедекинд, и пришел к мысли о задаче с подвохом.
НаградыПередо мной стояла трудная задача.
С самого начала я планировал, что максимальный балл будет ставится либо за правильное решение (что естественно) без излишеств, либо за полное описание всех выпуклых 15-реберных многогранников, все грани которых правильные многоугольники (даже если это описание будет снабжено выводом, ущемляющим Федю). За полное описание и правильный вывод "в одном флаконе" предполагались дополнительные баллы.
Но все оказалось не так просто. Например, Николай Дерюгин нашел все подходящие многогранники. И сделал правильный вывод. Но у меня сложилось впечатление, что основой этого вывода стала вычислительная ошибка при нахождении объема triangular cupola.
После мучительных раздумий баллы распределены так:
За правильное решение задачи Алексей Волошин получает 7 призовых баллов. Столько же получает Николай Дерюгин за более полное и формально тоже правильное решение. Виктор Филимоненков, Олег Полубасов и Анатолий Казмерчук получают по 6 призовых баллов, а Сергей Половинкин ("обнаруживший" пару лишних многогранников) - 5 призовых баллов (за один, "обнаоуженный" еще и ведущим, балл не снимался).
эстетическая оценка задачи - 4.1 балла