Точного источника задачи не знаю, давал преподаватель.
"На его месте должен был быть я" (с) Извиняюсь за некропостинг, но не смог пройти мимо (тоже предлагаю своим студентам эту задачу). Касательно первоисточника и точной формулировки задачи:
von zur Gathen & Gerhard in Modern Computer Algebra писал(а):
The fact that two random integers are coprime with probability

is a theorem of Dirichlet (1849). Dirichlet also proves the fact, surprising at first sight, that for fixed

in a division the remainder

, with

, is more likely to be smaller than

than larger: If
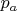
denotes the probability for the former, where

is chosen uniformly at random, then
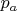
is asymptotically

.
Или зафиксировать первое число, а второе считать не большим его, выбираемым равновероятно. Тогда вероятность будет зависеть от первого числа.
Вот прям как у классика :)



