Написал полное решение, а потом подумал, что по правилам форума это нехорошо. Но стирать решение жалко. Поэтому я его просто спрячу под хайд, а ТС для начала дам подсказку: сведите всё к случаю

.
(Оффтоп)
Ортогональная проекция компакта - компакт, ортогональная проекция связного множества связна. Функция со значениями в

непрерывна тогда и только тогда, когда непрерывны её проекции на каждую из координат. Таким образом, достаточно рассмотреть случай
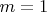
.
Пусть

такова, что переводит компакты в компакты и связные подмножества в связные. Пусть

разрывна в

. Тогда существует

, такое что для любого

найдётся

со свойством

и

. Значит, существует последовательность

элементов

, такая что

и либо

, либо

для всех

.
Рассмотрим первый случай

, второй рассматривается аналогично. Пусть

. Так как образ каждого

связен, то он содержит все числа из отрезка
![$[f(a) - \varepsilon, f(a)] \subseteq [f(x_k), f(a)]$ $[f(a) - \varepsilon, f(a)] \subseteq [f(x_k), f(a)]$](https://dxdy-04.korotkov.co.uk/f/b/1/2/b126e5a1144e8a7eac1b86bb545cc31882.png)
. Пусть

- строго убывающая последовательность чисел из отрезка
![$[f(a) - \varepsilon, f(a)]$ $[f(a) - \varepsilon, f(a)]$](https://dxdy-04.korotkov.co.uk/f/3/3/8/338fce19a0a5b0f8f13be3019029f74382.png)
, стремящаяся к

. Для каждого

выберем

такое, что

. Множество

компактно, однако образ

не может быть компактен в силу того, что он содержит все

-ые и не содержит

. Противоречие.
Кстати, вместо

в условии задачи можно было взять произвольное метрическое пространство. А вот

при

, похоже, существенно. По крайней мере, в придуманном мною доказательстве это используется. Интересно, можно ли подобрать метрическое пространство

с разрывной функцией

такое, что

сохраняет связность и компактность подмножеств

?
А если в условии задачи заменить

на произвольное гильбертово пространство, будет ли выполняться утверждение о непрерывности

? Или, если для гильбертовского ответ положительный, на произвольное банахово?



