Ещё раз хочу сказать спасибо за конкретные указания где и что почитать. Книжку я скачал и по мере наличия времени и возможности буду её изучать. Не судите строго, если я, не успев разобраться в каком-то моменте, буду задавать глупые вопросы.
Someone писал(а):
Вы очень усложняете вопрос. Если Вы вполне упорядочили множество действительных чисел, то множество

будет счётным (или конечным) для любого счётного (или конечного) ординала

, так что его заведомо можно занумеровать натуральными числами.
Это я понимаю. Просто я априорно не знал, какие ординалы являются счётными, и мне показалось, что наиболее убедительный способ прояснения этого вопроса - предложить конкретную процедуру нумерации.
Someone писал(а):
Но Вам хочется строить новую последовательность, используя ранее построенные, а сложность такого построения зависит от сложности рассматриваемого ординала.
Между тем, счётные ординалы могут быть устроены весьма сложно.
Думаю, здесь дело не только в сложности. Я ведь просто нумеровал ординалы в том порядке, в котором они следуют, - куда смог добраться, применяя индуктивные рассуждения, туда добрался. Вопрос в том, куда и, главное,
почему я не смогу добраться.
Someone писал(а):
В той книге, на которую я ссылался, определяются так называемые "эпсилоновые ординалы". Они получаются так. Берём любой конечный или счётный ординал

и определяем последовательность формулой

для

. Тогда

. Определяем

. Полученный таким образом ординал и называется эпсилоновым. Он счётный и удовлетворяет соотношению

.
Да, я прочитал. Как я понял, процедура нумерации заведомо проходит:
1. Через любые арифметические операции над ординалами: инкремент, сложение, умножение, возведение в степень. И даже через такую экзотическую арифметическую операцию

, как возведение ординала

в степень самого себя

раз, т.е.:

,

.
2. Через операцию взятия предела последовательности счётных ординалов

, где

, т.е. если

, то

- счётный ординал.
Соответственно, поскольку эпсилоновый ординал определяется как

, то он тоже счётный. Я правильно рассуждаю?
Someone писал(а):
epros писал(а):
Что касается недостижимости

счётными процедурами, то получается, что он недостижим и никакими "арифметическими" процедурами над
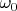
, т.е. вообще
никакая функция от
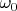
не даст нам

?
"Вообще никакая" - это, конечно, чересчур. Я имел в виду функции, значения которых на счётных ординалах являются также счётными ординалами, и точную верхнюю грань счётного множества счётных ординалов.
Как я понимаю, никакими арифметическими операциями (перечисленными выше) и операцией взятия предела последовательности счётных ординалов мы дальше ординала

не уйдём. Потому что и

, и

и даже

- всё это равно всё тому же

. Правильно?
Дальнейший вопрос для меня заключается вот в чём: Если ординал

(первого несчётного ординала), можно ли утверждать, что

?
К тому же мне пока так и не стало понятным,
что именно помешает нам построить процедуру нумерации таким образом, чтобы относительно утверждения

о счётности ординала

можно было утверждать:

? Раз "существует" процедура перехода от счётного множества к несчётному (взятие множества мощности), то, наверное, ей должна соответствовать и какая-то функция

над ординалами. Разве её нельзя выразить через арифметические операции и предел последовательности?
Например, для конечных ординалов эта функция:

. Почему её нельзя рассмотреть в пределе

и таким образом сопоставить операции взятия мощности для счётного множества функцию

над ординалами?
Someone писал(а):
Но мы ведь не можем получить
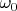
посредством
конечной процедуры. И получаем его после бесконечного числа шагов. Почему Вас удивляет, что первый несчётный ординал получается только после несчётного числа шагов?
Да, я хорошо понимаю, почему конечная процедура не доказывает

. Потому что она не даёт нам

, а значит мы не можем применить индукцию, даже если имеем

.
Someone писал(а):
Это смотря какое утверждение. Оно может быть таким, что на
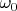
не распространяется (например, утверждение о конечности какого-нибудь множества, которое строится путём пошагового добавления попарно различных элементов). Такая же ситуация и для

: одни утверждения позволяют продолжать индукцию далее

, другие - нет (например, Ваше утверждение о счётности множества).
Честно говоря, не могу представить себе
ни одного утверждения относительно ординалов, которое бы можно было продолжить до

. Для этого необходимо иметь

, а где же мы его возьмём без каких-то соображений о том, что это такое за множество

?



