Трансфинитная индукция и непротиворечивость теории множеств

[epros]

Господа,
на данные мысли меня навёл парадокс Сколема. Как известно, суть его состоит в том, что если аксиомактика теории множеств изложена на языке логики первого порядка, то теория множеств имеет счётную модель (в которой однако можно определить несчётное множество).

Вроде бы считается, что парадокса "формально" как бы и нет. Сам Сколем, по крайней мере, трактовал его таким образом, что биекция $\mathbb{N} \leftrightarrow \mathbb{P}(\mathbb{N})$ не существует "в рамках модели" теории множеств, но существует где-то "за рамками её модели". Он даже формулировал это таким образом, что "биекция не является множеством".

Мне такое объяснение показалось весьма странным, ибо доказательство самой теоремы Лёвенхейма-Сколема проведено целиком и полностью в терминах теории множеств (в конце концов, само понятие "язык логики первого порядка" - теоретико-множественное). С другой стороны, сам подход, предполагающий построение т.н. "моделей" теории, показался мне достаточно искусственным. И у меня возникла мысль, а нельзя ли, используя неконструктивную аксиоматику, напрямую (т.е. без построения "моделей") доказать нечто, противоположное теореме Кантора? Естественно, если бы это было возможно, то, поскольку теорема Кантора тоже доказана, это бы непосредственно свидетельствовало о противоречивости аксиоматики.

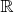
Засим предлагаю Вашему вниманию некую схему вывода (сразу предупреждаю, что не безупречную), основанную на предположении о применимости трансфинитной индукции к множеству $\mathbb{R}$, и прошу Вас указать на ошибку.

Сначала, во избежание недоразумений, сформулирую, что я понимаю под трансфинитной индукцией:
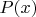Если множество $\mathbb{S}$ вполне упорядочено по некоему отношению $\leqslant $, а $P(x)$ - некое высказывание относительно $x \in \mathbb{S}$, то из $P(x_0)$, где $x_0$ - минимальный элемент $\mathbb{S}$, и из $(\forall y < x : P(y)) \to P(x)$ выводится $\forall x \in \mathbb{S} : P(x)$

В своём выводе я буду пользоваться понятием последовательности неотрицательных действительных чисел, определяемой как:
$A^{[m]} := \{(k,a_k^{[m]}) : k \in \mathbb{N} \wedge a_k^{[m]} \in [0,+\infty) \wedge \forall i,j : (i = j) \to (a_i^{[m]} = a_j^{[m]})\}$
Очевидно, что она же - отображение $\mathbb{N} \to \mathbb{R}$ (не обязательно однозначное). Здесь индекс $[m]$ не обязательно подразумевает целое число, а вообще-говоря является любым ординалом, по смыслу обозначающим "версию" последовательности.

Итак:
1. Возьмём множество $\mathbb{S} = [0,+\infty)$ с обычным отношением порядка для действительных чисел. Нетрудно убедиться, что оно вполне упорядочено.
2. Возьмём высказывание $P(x) = \exists A^{[m]} \verb
(Т.е. "Существует последовательность, содержащая все точки отрезка от 0 до x").
3. Нетрудно убедиться, что минимальным элементом является $x_0 = 0$
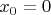
4. Определим нулевую версию последовательности как:
$A^{[0]} := \{(k,0) : k \in \mathbb{N}\}$
(т.е. последовательность из одних нулей). Нетрудно проверить, что она соответствует общему определению $A^{[m]}$
5. Нетрудно убедиться, что $\forall t \in [0,0] \verb, т.е. $P(0) = \exists A^{[m]} \verb выполнено.
6. Предположим, что $\forall y < x : P(y)$, т.е. $\forall y \in [0,x) \verb
6.1 Возможно, что это самый спорный момент вывода, но поскольку $(\forall y \in [0,x) \verb и поскольку каждому множеству $\mathbb{Y}$ из данной серии соответствует последовательность $A^{[m]}$, то должна существовать и последовательность $A^{[m]}$ для множества $\mathbb{X}$, т.е. $\exists A^{[m]} \verb
6.2 Дополним эту последовательность $A^{[m]}$ числом $x$ следующим образом:
$a_{k+1}^{[m+1]} := a_k^{[m]} \verb
$a_1^{[m+1]} := x$
Таким образом, последовательность $A^{[m+1]}$ включает все числа $\in [0,x]$, т.е. можно утверждать, что:
$\exists A^{[m]} \verb
(здесь изменение индекса версии последовательности не играет роли, поскольку формула утверждает существование некой версии последовательности)
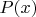
7. Поскольку предыдущая формула означает $P(x)$ и она была выведена из предположения $\forall y < x : P(y)$, то, применяя трансфинитную индукцию, мы можем записать, что: $\forall x \in [0,+\infty) \verb

Вывод проводился для неотрицательных действительных чисел, однако в него можно включить и отрицательные, выбрав в качестве отношения порядка сравнение модулей, а при равенстве модулей считать меньшим отрицательное число. В таком случае последняя формула записалась бы как:
$\forall x \in \mathbb{R} \verb

В переводе на нормальный язык это означает, что точки любого действительного отрезка могут быть пронумерованы. Конечно, я не настаиваю на корректности данного вывода. У меня вызывает подозрение пункт 6.1. Но как-то это всё кажется очень странным, что вопрос состоятельности аксиоматики зависит от таких тонкостей... Может быть существует прямой способ сделать вывод, противоположный выводу п. 6.1, т.е. что из $\forall y \in [0,x) \verb не следует $\exists A^{[m]} \verb?

[Someone]

epros писал(а):

1. Возьмём множество $\mathbb{S} = [0,+\infty)$ с обычным отношением порядка для действительных чисел. Нетрудно убедиться, что оно вполне упорядочено.

Определение вполне упорядоченного множества предъявите, пожалуйста.

[epros]

Someone писал(а):

epros писал(а):

1. Возьмём множество $\mathbb{S} = [0,+\infty)$ с обычным отношением порядка для действительных чисел. Нетрудно убедиться, что оно вполне упорядочено.

Определение вполне упорядоченного множества предъявите, пожалуйста.

Ну, наверное я неправ в том, что "нетрудно убедиться", но ведь есть теорема Цермело, утверждающая, что любое множество можно вполне упорядочить. Действительно, обычное отношение порядка не подходит, поскольку не всякое подмножество имеет минимальный элемент. Ну, тогда нужно взять не обычное отношение порядка, а то, которое "существует" согласно Цемерло. Тогда в качестве высказывания следует взять:
$$P(x) = \exists A^{[m]} \verb

[Someone]

epros писал(а):

Ну, тогда нужно взять не обычное отношение порядка, а то, которое "существует" согласно Цемерло. Тогда в качестве высказывания следует взять:
$$P(x) = \exists A^{[m]} \verb

Здесь "$\leqslant$" - в смысле этого полного отношения порядка, или в смысле естественного отношения порядка на множестве действительных чисел?

Перепишите всё доказательство соответствующим образом. Если Вы берёте новое отношение порядка, то старые обозначения не годятся.

[epros]

Someone писал(а):

epros писал(а):

Ну, тогда нужно взять не обычное отношение порядка, а то, которое "существует" согласно Цемерло. Тогда в качестве высказывания следует взять:
$$P(x) = \exists A^{[m]} \verb

Здесь "$\leqslant$" - в смысле этого полного отношения порядка, или в смысле естественного отношения порядка на множестве действительных чисел?

Перепишите всё доказательство соответствующим образом. Если Вы берёте новое отношение порядка, то старые обозначения не годятся.

В смысле полного отношения порядка. ОК, попробую переписать:

1. Возьмём множество $\mathbb{R}$ с отношением полного порядка $\leqslant$ (существующим в силу теоремы Цемерло). Как обычно, будем писать $a < b$ если $a \leqslant b \wedge \overline{(a \geqslant b)}$
2. Возьмём высказывание $P(x) = \exists A^{[m]} \verb
(Т.е. "Существует последовательность, содержащая все элементы не больше $x$").
3. Определим нулевую версию последовательности как: $A^{[0]} := \{(k,x_0) : k \in \mathbb{N}\}$, где $x_0$ - минимальный элемент $\mathbb{R}$. Т.е. вся последовательность состоит из бесконечного повторения минимального элемента ($a_k^{[0]} = x_0$). Нетрудно проверить, что она соответствует общему определению $A^{[m]}$
4. Поскольку из $t \leqslant x_0$ следует $t = x_0$, то $\forall t \leqslant x_0 \verb, т.е. $P(x_0) = \exists A^{[m]} \verb выполнено.
5. Предположим, что $\forall y < x : P(y)$, т.е. $\forall y < x \verb
5.1 Возможно, что это самый спорный момент вывода, но поскольку $(\forall y < x \verb и поскольку каждому множеству $\mathbb{Y}$ из данной серии соответствует последовательность $A^{[m]}$, то должна существовать и последовательность $A^{[m]}$ для множества $\mathbb{X}$, т.е. $\exists A^{[m]} \verb
5.2 Дополним эту последовательность $A^{[m]}$ числом $x$ следующим образом:
$a_{k+1}^{[m+1]} := a_k^{[m]} \verb
$a_1^{[m+1]} := x$
Таким образом, последовательность $A^{[m+1]}$ включает все числа $\leqslant x$, т.е. можно утверждать, что:
$\exists A^{[m]} \verb
(здесь изменение индекса версии последовательности не играет роли, поскольку формула утверждает существование некой версии последовательности)
7. Поскольку предыдущая формула означает $P(x)$ и она была выведена из предположения $\forall y < x : P(y)$, то, применяя трансфинитную индукцию, мы можем записать, что: $\forall x \in \mathbb{R} \verb

В переводе на человеческий язык: Множество действительных чисел, меньших чем любое заданное число, счётно.

Конечно, "меньших" здесь в смысле отношения полного порядка на $\mathbb{R}$. Мда, даже в самом лучшем случае это с теоремой Кантора никак не конфликтует...

[Someone]

epros писал(а):

5. Предположим, что $\forall y < x : P(y)$, т.е. $\forall y < x \verb
5.1 Возможно, что это самый спорный момент вывода, но поскольку $(\forall y < x \verb и поскольку каждому множеству $\mathbb{Y}$ из данной серии соответствует последовательность $A^{[m]}$, то должна существовать и последовательность $A^{[m]}$ для множества $\mathbb{X}$, т.е. $\exists A^{[m]} \verb

Не пройдёт уже на первом бесконечном ординале. Вы построите (пользуясь методом 5.2) последовательности $A^{[0]},A^{[1]},A^{[2]},\dots,A^{[m]},\dots$, покрывающие, соответственно, множества, содержащие $1,2,3,\dots,m+1,\dots элементов $a^{[0]}_1,a^{[1]}_1,a^{[1]}_1,\dots,a^{[m]}_1,\dots$. Откуда возьмётся последовательность, содержащая все эти элементы?

Со счётными ординалами, естественно, справиться можно (объединение счётного множества счётных множеств есть счётное множество). Но что будете делать на первом несчётном шаге своего построения?

[epros]

Someone писал(а):

Со счётными ординалами, естественно, справиться можно (объединение счётного множества счётных множеств есть счётное множество). Но что будете делать на первом несчётном шаге своего построения?

Применять трансфинитную индукцию, не заботясь о том, "счётный" шаг или "несчётный".

По правде говоря, я не уверен в выводе $\exists A^{[m]} \verb из $\forall y < x \verb (п.5.1), поэтому я не могу считать весь вывод правильным.

Но что касается довода о счётности или несчётности ординалов, то он мне непонятен. Ординалы я использую только для нумерации последовательностей (чтобы отличать их друг от друга), мне без разницы какой именно ординал нумерует какую последовательность (счётный или несчётный). В конце концов, существует континуум последовательностей действительных чисел, а в силу теоремы Цемерло его можно вполне упорядочить, т.е. приписать каждой из них ординал. Моя процедура выбирает из этого континуума последовательностей некое подмножество. Счётное? Не знаю, и не задаюсь этим вопросом. Моя задача - доказать вывод о том, что существует такая последовательность, что...

[Someone]

epros писал(а):

По правде говоря, я не уверен в выводе $\exists A^{[m]} \verb из $\forall y < x \verb (п.5.1), поэтому я не могу считать весь вывод правильным.

А у Вас нет никакого вывода этого утверждения. Вы его просто формулируете, а оно отнюдь не очевидно. Я же Вас просил посмотреть первый бесконечный шаг: откуда там берётся эта последовательность? Там очень хорошо видно, что её нет, и что её нужно строить. А когда Вы начнёте строить, то и увидите разницу между счётными и несчётными шагами.

[epros]

Someone писал(а):

epros писал(а):

По правде говоря, я не уверен в выводе $\exists A^{[m]} \verb из $\forall y < x \verb (п.5.1), поэтому я не могу считать весь вывод правильным.

А у Вас нет никакого вывода этого утверждения. Вы его просто формулируете, а оно отнюдь не очевидно.

Да, это так. Но мне почему-то кажется, что должен существовать какой-то способ сделать данный вывод (настолько это простая вещь - по крайнем мере, более очевидная, чем аксиома выбора).

Someone писал(а):

Я же Вас просил посмотреть первый бесконечный шаг: откуда там берётся эта последовательность? Там очень хорошо видно, что её нет, и что её нужно строить. А когда Вы начнёте строить, то и увидите разницу между счётными и несчётными шагами.

Насколько я понимаю, "первому бесконечному шагу" предшествует бесконечное количество "конечных", в результате которых какая-то последовательность была построена?

[Someone]

epros писал(а):

Да, это так. Но мне почему-то кажется, что должен существовать какой-то способ сделать данный вывод (настолько это простая вещь - по крайнем мере, более очевидная, чем аксиома выбора).

Существует: построить последовательность, если это возможно.

epros писал(а):

Someone писал(а):

Я же Вас просил посмотреть первый бесконечный шаг: откуда там берётся эта последовательность? Там очень хорошо видно, что её нет, и что её нужно строить. А когда Вы начнёте строить, то и увидите разницу между счётными и несчётными шагами.

Насколько я понимаю, "первому бесконечному шагу" предшествует бесконечное количество "конечных", в результате которых какая-то последовательность была построена?

Нету этой последовательности. Не построена она. Построена последовательность последовательностей: первая последовательность покрывает один элемент, вторая - два, третья - три,... А последовательности, покрывающей все элементы $\{a^{[m]}_1:m<\omega_0\}$ , нет: любая из уже построенных последовательностей покрывает лишь конечное число элементов.

И почему Вы это у меня спрашиваете? Вы пытаетесь что-то доказать, поэтому Вашей обязанностью и является предъявление этой последовательности (хотя бы и неконструктивным способом).

[epros]

Someone писал(а):

epros писал(а):

Да, это так. Но мне почему-то кажется, что должен существовать какой-то способ сделать данный вывод (настолько это простая вещь - по крайнем мере, более очевидная, чем аксиома выбора).

Существует: построить последовательность, если это возможно.

Мне это непонятно.

Someone писал(а):

epros писал(а):

Насколько я понимаю, "первому бесконечному шагу" предшествует бесконечное количество "конечных", в результате которых какая-то последовательность была построена?

Нету этой последовательности. Не построена она. Построена последовательность последовательностей: первая последовательность покрывает один элемент, вторая - два, третья - три,... А последовательности, покрывающей все элементы $\{a^{[m]}_1:m<\omega_0\}$ , нет: любая из уже построенных последовательностей покрывает лишь конечное число элементов.

Почему Вы это с такой уверенностью заявляете?

А если я возьму в качестве отношения полного порядка следующее:
1. Пронумерую натуральными числами все рациональные числа (согласно известной диагональной процедуре).
2. Множество оставшихся чисел, т.е. $\mathbb{R} \verb, буду нумеровать начиная с первого трансфинитного ординала $\omega_0$.

Вы по-прежнему будете утверждать, что последовательности, покрыващей все элементы до $\omega_0$, "не существует"? Но ведь такое утверждение означало бы, что рациональные числа не были пронумерованы!

Someone писал(а):

И почему Вы это у меня спрашиваете? Вы пытаетесь что-то доказать, поэтому Вашей обязанностью и является предъявление этой последовательности (хотя бы и неконструктивным способом).

Ну как, "предъявил"?

Кстати, я не согласен с Вами, что я должен "предъявить" что-то, помимо самого вывода. Многие неконструктивные доказательства строятся на утверждениях о существовании каких-то объектов, которых никто не может "предъявить".

[Someone]

epros писал(а):

Someone писал(а):

epros писал(а):

Насколько я понимаю, "первому бесконечному шагу" предшествует бесконечное количество "конечных", в результате которых какая-то последовательность была построена?

Нету этой последовательности. Не построена она. Построена последовательность последовательностей: первая последовательность покрывает один элемент, вторая - два, третья - три,... А последовательности, покрывающей все элементы $\{a^{[m]}_1:m<\omega_0\}$ , нет: любая из уже построенных последовательностей покрывает лишь конечное число элементов.

Почему Вы это с такой уверенностью заявляете?

А какие последовательности у нас к этому моменту построены? И что каждая из них покрывает?

epros писал(а):

А если я возьму в качестве отношения полного порядка следующее: ...

А какая разница?

epros писал(а):

Вы по-прежнему будете утверждать, что последовательности, покрыващей все элементы до $\omega_0$, "не существует"? Но ведь такое утверждение означало бы, что рациональные числа не были пронумерованы!

Я утверждал совсем другое: не то, что такой последовательности не существует, а то, что её нет среди уже построенных. В частности, Ваша нумерация рациональных чисел к делу отношения не имеет: её нет в множестве построенных последовательностей $\{A^{[m]}:m<\omega_0\}$.

epros писал(а):

Someone писал(а):

И почему Вы это у меня спрашиваете? Вы пытаетесь что-то доказать, поэтому Вашей обязанностью и является предъявление этой последовательности (хотя бы и неконструктивным способом).

Ну как, "предъявил"?

Пока нет. Даже для простейшего случая первого бесконечного ординала.

epros писал(а):

Кстати, я не согласен с Вами, что я должен "предъявить" что-то, помимо самого вывода. Многие неконструктивные доказательства строятся на утверждениях о существовании каких-то объектов, которых никто не может "предъявить".

Я же оговорился: хотя бы и неконструктивным способом. Хоть "от противного". Здесь "предъявить" означает всего лишь "доказать существование". В Вашем рассуждении такого доказательства нет, поэтому ни один математик Ваше построение не признает.

[epros]

Someone писал(а):

А какие последовательности у нас к этому моменту построены? И что каждая из них покрывает?

Построена $A^{[m]}$, которая покрывает $\forall t \leqslant y$, где $y$ - любое число с номером $< \omega_0$.

Someone писал(а):

Я утверждал совсем другое: не то, что такой последовательности не существует, а то, что её нет среди уже построенных. В частности, Ваша нумерация рациональных чисел к делу отношения не имеет: её нет в множестве построенных последовательностей $\{A^{[m]}:m<\omega_0\}$.

Возможно, я не доказал, что "нумерующая последовательность есть среди построенных", но разве Вы доказали, что её "нет среди построенных"?

Someone писал(а):

Здесь "предъявить" означает всего лишь "доказать существование". В Вашем рассуждении такого доказательства нет, поэтому ни один математик Ваше построение не признает.

Ну я и не утверждаю, что доказательство безупречно. Пункт 5.1 явно не доказан. Но согласитесь, что если бы вывод 5.1 можно было бы сделать, то существование последовательности - предшественника $A^{[\omega_0]}$ было бы доказано?

[Someone]

epros писал(а):

Someone писал(а):

А какие последовательности у нас к этому моменту построены? И что каждая из них покрывает?

Построена $A^{[m]}$, которая покрывает $\forall t \leqslant y$, где $y$ - любое число с номером $< \omega_0$.

Неверно. $A^{[m]}$, $m<\omega_0$, покрывает не то, что Вы написали. Она - в соответствии с Вашим построением - покрывает множество $\{a^{[0]}_1,{a^{[1]}_1,{a^{[2]}_1,\dots,{a^{[m]}_1\}$, и ничего больше не покрывает. В частности, тут нет никакого любого числа $y$ с номером $<\omega_0$.

epros писал(а):

Someone писал(а):

Я утверждал совсем другое: не то, что такой последовательности не существует, а то, что её нет среди уже построенных. В частности, Ваша нумерация рациональных чисел к делу отношения не имеет: её нет в множестве построенных последовательностей $\{A^{[m]}:m<\omega_0\}$.

Возможно, я не доказал, что "нумерующая последовательность есть среди построенных", но разве Вы доказали, что её "нет среди построенных"?

Запросто. Но это настолько очевидно, что я надеялся, что Вы сами это увидите.
Множество построенных последовательностей в данный момент есть $\{A^{[m]}:m<\omega_0\}$. Берём любое $m<\omega_0$. Покрывает ли последовательность $A^{[m]}$ бесконечное множество $\{a^{[n]}:n<\omega_0\}$? Нет, не покрывает, так как, согласно построению, она покрывает конечное множество $\{a^{[0]}_1,{a^{[1]}_1,{a^{[2]}_1,\dots,{a^{[m]}_1\}$, и ничего больше не покрывает. В частности, $a^{[m+1]}_1\notin\{a^{[0]}_1,{a^{[1]}_1,{a^{[2]}_1,\dots,{a^{[m]}_1\}$, так как, по предположению, $a^{[0]}_1<a^{[1]}_1<a^{[2]}_1<\ldots<a^{[m]}_1<a^{[m+1]}_1$. То есть, никакая из построенных последовательностей не покрывает множество $\{a^{[n]}:n<\omega_0\}$, и Вы не можете продолжить своё построение на шаге $\omega_0$.

epros писал(а):

Ну я и не утверждаю, что доказательство безупречно. Пункт 5.1 явно не доказан.

Этого достаточно. Доказательства нет, и обсуждать нечего.

[epros]

А ведь Вы своими соображениями про первый трансфинитный ординал навели меня на кое-какие мысли о том, как модифицировать мой алгоритм нумерации R (да и любого множества, на самом-то деле), чтобы он заведомо проходил через предельные ординалы.

Давайте только я сначала изложу свое понимание некоторых свойств ординалов (поправьте пожалуйста, если я в чём-то ошибусь):
1. Любой ординал $\alpha$ имеет последователя $\alpha + 1$
2. Любой ординал $\alpha$ либо является предельным (не является последователем никакого ординала), либо не является предельным (является чьим-то последователем).
3. Цепочка последователей любого ординала $\alpha$ составляет счётное множество: $\{\alpha, \alpha + 1, \alpha + 2, ...\}$.

Итак, алгоритм таков:
1. Возьмём некое множество $\mathbb{S}$ с отношением полного порядка на нём. Это означает, что каждый его элемент $x$ имеет уникальный ординальный номер $\alpha$. Будем обозначать такой элемент как $x_{\alpha}$.
2. Определяем $A^{[0]}$ как бесконечную последовательность $\{x_0, x_1, x_2, ...\}$ элементов, имеющих финитные ординальные номера.
3. Рассмотрим множество $\mathbb{S} \verb элементов, не вошедших в последовательность. Оно есть подмножество вполне упорядоченного множества, а потому вполне упорядочено. В частности, оно имеет минимальный элемент $x_{\omega 0}$.
3. Определяем $B^{[\omega 0]}$ как бесконечную последовательность $\{x_{\omega 0}, x_{\omega 1}, x_{\omega 2}, ...\}$ элементов, имеющих номера из цепочки последователей ординала $\omega 0$.
4. Определяем $A^{[\omega 0]}$ как бесконечную последовательность $\{x_0, x_{\omega 0}, x_1, x_{\omega 1}, x_2, x_{\omega 2}, ...\}$. Очевидно, что она включает все элементы с номерами до $\omega 0 + \omega 0$ (не включительно).

Далее рассуждаем по индукции:
5. Предполагаем, что для данного элемента $x_{\alpha}$ множества $\mathbb{S}$ существует последовательность $C^{[\alpha]} = \{c_0^{[\alpha]}, c_1^{[\alpha]}, c_2^{[\alpha]}, ...\}$, такая что:
- Если номер элемента $\alpha$ является предельным ординалом, то последовательность $C^{[\alpha]}$ включает все элементы множества $\mathbb{S}$, меньшие, чем $x_{\alpha}$.
- А если номер элемента $\alpha$ не является предельным ординалом, то последовательность $C^{[\alpha]}$ включает все элементы множества $\mathbb{S}$, меньшие, чем $x_{\alpha}$, а также все элементы $x_{\alpha}, x_{\alpha + 1}, x_{\alpha + 2}, ...$ с номерами, составляющими цепочку последователей ординала $\alpha$.
5.1 Если $\alpha$ - не предельный ординал, то определяем $A^{[\alpha]} := C^{[\alpha]}$ (последовательность уже включает $x_{\alpha}$).
5.2. Если $\alpha$ - предельный ординал, то определяем $A^{[\alpha]} := \{c_0^{[\alpha]}, x_{\alpha}, c_1^{[\alpha]}, x_{\alpha + 1}, c_2^{[\alpha]}, x_{\alpha + 2}, ...\}$.
6. Поскольку в обоих случаях из предположения (5) следует существование последовательности $A^{[\alpha]}$, включающей все элементы по $x_{\alpha}$ включительно, то по правилу трансфинитной индукции это означает, что существует последовательность, включающая все элементы множества $\mathbb{S}$.

Ну, что теперь скажете?