О, отлично! "Собственные попытки решения" у Вас уже есть, и Вы на правильном пути.
Полная кинетическая энергия системы

общая для обоих уравнений. Она состоит из двух слагаемых: кинетическая энергия пластинки и кинетическая энергия грузика. В принципе, каждое слагаемое может зависеть и от

, и от

, и даже от

и

, поэтому лучше обозначать их не

и

, а как-то вроде

и

.
Кинетическую энергию пластинки Вы нашли правильно:

.
С грузиком сложнее. Он участвует сразу в двух вращениях -- вокруг вертикальной оси и вокруг горизонтальной. Ваша формула была бы верна, если бы грузик только двигался по каналу в плоскости неподвижной пластинки. Но пластинка и сама вращается, сообщая грузику дополнительную переносную скорость. Вектор скорости движения грузика равен сумме:
-- вектора скорости движения грузика относительно пластинки; он лежит в плоскости пластинки, его модуль равен

;
-- вектора переносной скорости; он перпендикулярен пластинке, его модуль равен

(понятно, откуда

?).
Раз эти векторы перпендикулярны, квадрат суммы по теореме Пифагора равен сумме квадратов. Результат:


Поэтому полная кинетическая энергия равна

.
Второй вопрос -- как учесть силы. Это можно сделать двумя способами.
1) включить в уравнение, соответствующее координате

, слагаемое

, ну, а в

включить соответствующее этой силе слагаемое;
2) записать обобщенную силу
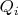
в правой части уравнения, соответствующего

.
Я вижу, что Вы выбрали второй способ. Но первый тоже хороший. Он годится для потенциальных сил. В нашем случае обе силы потенциальные -- сила тяжести, действующая на грузик, и момент, действующий на пластину. Потенциальная энергия равна

, и теперь надо всё подставить в уравнения
![$$\left\{\begin{array}{l}\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{\theta}} -\dfrac{\partial T}{\partial {\theta}}=- \dfrac {\partial U}{\partial \theta}\\[2.5ex]\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{\varphi}} -\dfrac{\partial T}{\partial {\varphi}}=- \dfrac {\partial U}{\partial \varphi}\end{array}\right.$$ $$\left\{\begin{array}{l}\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{\theta}} -\dfrac{\partial T}{\partial {\theta}}=- \dfrac {\partial U}{\partial \theta}\\[2.5ex]\dfrac{d}{dt} \dfrac{\partial T}{\partial \dot{\varphi}} -\dfrac{\partial T}{\partial {\varphi}}=- \dfrac {\partial U}{\partial \varphi}\end{array}\right.$$](https://dxdy-01.korotkov.co.uk/f/4/2/d/42d640562a8e3290f1c9e476ab9efa7a82.png)
Rage2304 писал(а):
Еще в голове вертится мысль, что (как минимум) для первого уравнения системы нужно вводить функцию Лагранжа L=T-П, т.к на груз, движущийся по кольцу - действует сила тяжести!!! Но это опять же все только мои наивные догадки =) В общем с нетерпением жду ваших комментариев!
Догадка Ваша была верной, и я эту силу учёл. Что касается

, то при желании мы можем писать эту букву вместо

, и уравнения станут ещё красивее:

Но с точки зрения решения задачи это будет шаг назад, к более абстрактной форме.