Матрица плотности - это идеологически очень простая штука. КМ можно записывать как для векторов состояния, так и для матриц плотности, и во многих случаях это будут эквивалентные способы представления.
Вектор состояния - это вектор, представим себе его как вектор-столбец
![$$\psi_i=\left[\begin{array}{c}\psi_1\\\vdots\\\psi_n\end{array}\right]=\lvert\psi\rangle.$$ $$\psi_i=\left[\begin{array}{c}\psi_1\\\vdots\\\psi_n\end{array}\right]=\lvert\psi\rangle.$$](https://dxdy-02.korotkov.co.uk/f/5/9/a/59ac893cc77eb77bf6efa34a370a76df82.png)
Вы знаете, что если вектор-строку умножить на вектор-столбец, получится скалярное произведение. Но можно заметить, что если их умножить в обратном порядке, вектор-столбец на вектор-строку, то получится матрица

Мы можем проделать эту операцию для вектора с самим собой (точнее, с его сопряжённым):
![$$\psi_i\psi_j^\dagger=\left[\begin{array}{c}\psi_1\\\vdots\\\psi_n\end{array}\right]\left[\begin{array}{ccc}\psi_1^*&\ldots&\psi_n^*\end{array}\right]=\left[\begin{array}{ccc}\psi_1\psi_1^*&\ldots&\psi_1\psi_n^*\\\vdots&\ddots&\vdots\\\psi_n\psi_1^*&\ldots&\psi_n\psi_n^*\end{array}\right]=\lvert\psi\rangle\langle\psi\rvert.$$ $$\psi_i\psi_j^\dagger=\left[\begin{array}{c}\psi_1\\\vdots\\\psi_n\end{array}\right]\left[\begin{array}{ccc}\psi_1^*&\ldots&\psi_n^*\end{array}\right]=\left[\begin{array}{ccc}\psi_1\psi_1^*&\ldots&\psi_1\psi_n^*\\\vdots&\ddots&\vdots\\\psi_n\psi_1^*&\ldots&\psi_n\psi_n^*\end{array}\right]=\lvert\psi\rangle\langle\psi\rvert.$$](https://dxdy-02.korotkov.co.uk/f/1/3/1/1315775659b13d3a0a6b1c7d43b8bd7982.png)
В такой матрице много элементов, глаза разбегаются, но суть её легко понять, если рассмотреть её как оператор (часто так прямо и обсуждают
оператор плотности). Что будет, если умножить её слева на произвольный вектор-столбец? Вектор-строка

умножится на него, дав скалярное произведение, а последующий за ним вектор-столбец

умножится на это скалярное произведение как на численный коэффициент. Итого, наш произвольный вектор-столбец будет рассмотрен в проекции на ось, и потом заменён на вектор вдоль этой оси, длиной в проекцию. То есть, наш оператор - это ровно
проектор на направление, заданное исходным вектором состояния

Очевидно, он несёт столько же информации (у нас, может быть, потерялась комплексная фаза, но она в КМ и не нужна, поскольку не имеет физического смысла).
Саму КМ записать для нового способа представления просто: если у нас раньше был любой оператор эволюции
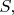
действовавший

то теперь мы так же можем подействовать и на матрицу плотности:

Если раньше мы вычисляли среднее значение наблюдаемой как

то сейчас должны взять
![$\operatorname{Tr}[f\lvert\psi\rangle\langle\psi\rvert].$ $\operatorname{Tr}[f\lvert\psi\rangle\langle\psi\rvert].$](https://dxdy-01.korotkov.co.uk/f/0/3/2/032d22be2aac42fe756a544440e2609f82.png)
Разумеется, и от базиса к базису (в КМ терминологии - "от представления к представлению") мы тоже можем переходить без проблем. Вот и всех отличий.
Но на самом деле аппарат матрицы плотности шире по возможностям, чем аппарат векторов состояния. Если мы проделаем любые операции сложения с векторами состояния, мы снова получим вектор состояния - мы можем перейти от
чистого состояния только к
суперпозиции, которая в другом базисе снова будет
чистым состоянием. Если же мы возьмём две матрицы плотности, то мы можем получить из них (просто линейной комбинацией) новую матрицу, которая по свойствам будет не хуже, чем исходные, но не будет отвечать никакому
чистому состоянию, а будет называться
смесью.
Теперь, зачем это нужно. Есть три примера, которые по сути исчерпывают три направления приложения матриц плотности (во всех остальных случаях достаточно использовать КМ в виде векторов состояния). Книга Блума упоминает только одно из них, ЛЛ-3 - другое только одно.
Например:Пусть у нас есть квантовая система, состоящая из нескольких подсистем, например, две взаимодействующие между собой частицы. Если мы сосредоточим своё внимание только на одной подсистеме (на одной частице), то мы не сможем описать её вектором состояния - не всегда её состояние будет чистым. Чтобы рассматривать её эволюцию и наблюдаемые, нужно записать её состояние как матрицу плотности.
Например:Пусть у нас есть квантовая статистическая система, которая находится случайно в одном из множества состояний, мы не знаем, в каком. Тогда, чтобы описать её свойства, мы должны снова прибегнуть к матрице плотности, считая её взвешенной суммой чистых состояний, где веса - вероятности. Такое описание необходимо, когда мы рассматриваем систему, не замкнутую, а находящуюся в тепловом контакте с окружением (при конечной температуре).
Например:Пусть мы экспериментаторы, и приготавливаем квантовую систему в каком-то состоянии (на начало квантового эксперимента). У нас могут быть способы приготовить систему в чистом состоянии, так, чтобы были точно заданы все её квантовые числа; а могут быть способы приготовить её в состоянии смеси, так что мы каких-то квантовых чисел не знаем. Например, пусть у нас есть способ излучить фотон, но неизвестной поляризации. Тогда в базисе состояний поляризации наш фотон приходится описать матрицей плотности, считая его дополнительные состояния поляризации равновероятными.



