(Оффтоп)
Прошу прощение за долгое отсутствие. Все выходные был занят тем, что активно не курил. Сегодня уже подаю признаки социальности

)))
Рассмотрим алгебру
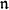

(не путать

с
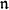
) матриц у которых все элементы, находящиеся ниже диагонали равны нулю включая и саму диагональ.
Легко проверить, что если
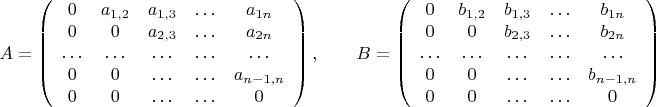
то
![$$[A,B]=\left(\begin{array}{ccccc}0 & 0 & c_{1,3} & \ldots & c_{1n}\\ 0 & 0 & 0 & \ldots & c_{2n} \\ \ldots &\ldots& \ldots &\ldots&\ldots \\ 0 & 0 & \ldots & \ldots & 0\\
0 & 0 &\ldots &\ldots &0 \end{array}\right),$$ $$[A,B]=\left(\begin{array}{ccccc}0 & 0 & c_{1,3} & \ldots & c_{1n}\\ 0 & 0 & 0 & \ldots & c_{2n} \\ \ldots &\ldots& \ldots &\ldots&\ldots \\ 0 & 0 & \ldots & \ldots & 0\\
0 & 0 &\ldots &\ldots &0 \end{array}\right),$$](https://dxdy-04.korotkov.co.uk/f/3/9/3/393b409a29d74157c7d828a8d429623e82.png)
т.е.
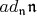
- множество всех матриц, у которых "нулевая диагональ смещена вверх". Таким же образом убеждаемся, что
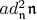
поднимает эту "диагональ" еще на ступеньку выше, и.т.д. Таким образром
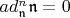
.
Чтобы получить факторалгебру
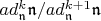
мы должны отождествить все элементы из
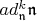
, разность которых принадлежит
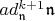
. Т.е. две матрицы с одинаковой

- й "диагональю" неразличимы. Так что, за представителя
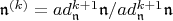
берем матрицу
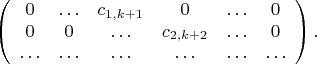
Отсюда сразу ясно, что, как линейное пространство,
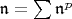
.
Правильно?



