Последний пример... В физике частиц особое место занимают компактные группы Ли. Такие и только такие группы могут описывать внутренние (калибровочные) симметрии. Классификация компактных групп Ли хорошо известна. Всякая такая группа разлагается в прямое произведение своего центра (абелевой группы) и простых компактных (неабелевых) групп Ли. Причем, три бесконечные последовательности групп

,

,

и пять исключительных групп

,
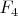
,

,

,

составляют все неизоморфные компактные простые группы Ли.
С другой стороны... Пусть

- композиционная ассоциативная алгебра с делением, т.е. одна из алгебр вида

,

или

. Определим на

-мерном векторном пространстве

скалярное произведение

Обозначим группу изометрий пространства

на себя символом

и отождествим каждую изометрию с матрицей, столбцы которой являются образами векторов стандартного базиса. Тогда легко показать, что матрица

тогда и только тогда принадлежит группе

, когда

где

- единичная матрица, а

- матрица, получающаяся из

транспонированием и заменой всех элементов на сопряженные (под сопряжением понимается инволюция алгебры

). В том случае, когда

,

или

, группа

,

или

соответственно, т.е. является ортогональной, унитарной или симплектической группой Ли. Подобным, но более сложным способом, с алгеброй октонионов

можно связать компактные группы Ли

,
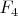
,

,

,

.
Таким образом, алгебры

,

,

,

присутствуют и здесь...



