С таким же результатом можно поменять знаки у трех слагаемых в выражении для квадрата интервала Минковского и констатировать, что при этом оно совпадает с выражением для квадрата четырехмерного евклидова пространства. Связи рассматриваемого пространства с пространством Минковского или евклидовым нет никакой.
С самим пространством Минковского - да, никакой. Но я писал о квадрате интервала, т. е. геометрии с метрикой четвёртой степени. Чтобы получить "правильные знаки", нужно чтобы модуль определялся следующим выражением:
![$|C_2|^4=[(-x^2+y^2)+(z^2+w^2)]^2=x^4+y^4+z^4+w^4-2x^2y^2-2x^2z^2-2x^2w^2+2y^2z^2+2y^2w^2+2z^2w^2$ $|C_2|^4=[(-x^2+y^2)+(z^2+w^2)]^2=x^4+y^4+z^4+w^4-2x^2y^2-2x^2z^2-2x^2w^2+2y^2z^2+2y^2w^2+2z^2w^2$](https://dxdy-01.korotkov.co.uk/f/c/e/b/ceb24af5783d3d0cbcee0a60876e776c82.png)
Есть подозрение, что его можно добиться соответствующим выбором образующих из алгебры бикомплексных чисел. Правда, базис при этом останется ортогональным, а не изотропным, поэтому пока никаких выводов отсюда делать не стоит

Это Вы нашли выражение для модуля бикомплексного числа в базисе, являющемся финслеровым аналогом ортонормированного. Попробуйте теперь тоже самое сделать в изотропном базисе.
Теперь касательно изотропных векторов. Изложу процедуру поиска. Итак, для начала, по аналогии с двойными числами, берём биссектриссы положительных "октантов" (8 положительных и 8 отрицательных, в сумме - 16). Эти 8 биссектрисс оказываются "эллиптического" и "гиперболического" типа:

;

;

;

;

;

;

;

.
Далее всё просто, хотя пересчёт определённое время занял. Итак, изотропные вектора выражаются через биссектриссы следующим элементарным образом:

;

;

;

.
Легко убедиться, что так введённые изотропные векторы удовлетворяют основному свойству изотропии:
![$e_je_le_me_n=
\left\{\begin {array}{1}
e_j, if [j=l=m=n],\\
0, otherwise.
\end {array}\right.
$ $e_je_le_me_n=
\left\{\begin {array}{1}
e_j, if [j=l=m=n],\\
0, otherwise.
\end {array}\right.
$](https://dxdy-04.korotkov.co.uk/f/b/e/6/be6a153fb51283f8da801bd05739378182.png)
Если я нигде выше не ошибся, что совершенно не исключено, выходит, что в изотропном базисе выражения, записанные в алгебре

оказываются абсолютно аналогичными таковым в
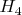
, а всё различие, довольно значительное, кстати, проявляется в виде матрицы перехода и виде выражения в ортонормированном (трансверсальном) базисе. Ну и, понятно, что индикатрисса, будучи такой же 16-связной , имеет другой совершенно вид...



