У меня
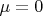
, так как средняя гравитационная плотность равна нулю из-за равного количества гравитационных зарядов противоположных знаков. Что именно Вас не устраивает?
Нет, в ньютоновской теории никаких "отрицательных зарядов" нет, а в Вашей пока ещё несуществующей теории в таком случае никакой гравитации вообще нет, всё компенсируется.
Так оно и есть. В нестационарной Вселенной о "ньютоновском потенциале" можно говорить с большой натяжкой
Дык, вообще нельзя. И не только в космологии, но и во многих других случаях. Его худо-бедно можно использовать в первом, наинизшем приближении для слабых медленно меняющихся полей, а чуть поточнее захочется - не хватит ньютоновского потенциала. Там сразу же ещё другие параметры появляются.
Если же учесть запаздывавание сигнала от одной точки к другой, то всё смещение частоты будет за счёт изменения потенциала, которое произойдёт за это время.
Дык, в нестационарной Вселенной этот Ваш "потенциал" всегда и везде равен нулю. Его как ни вычитай, ничего, кроме нуля, не получится.
Так происходит в нестационарной сфере.
А в нестационарной сфере иначе. Там вне сферы и внутри поле статическое. По теореме Биркгофа.
Я имел ввиду, что не только наблюдатели внутри сферы, но и во всём пространстве испытывают такие же физические (гравитационные) процессы, как и внутри сферы.
А внутри сферы никаких "физических гравитационных процессов" не происходит. Там статическое поле. Ничего не меняется.
Интервалы для Вселенных с ненулевой пространственной кривизной записываются в полярных координатах, и только для плоского случая в декартовых.
Не в полярных, а в сферических.
Но это ерунда. Можно записать и в "декартовых", только выглядеть будет сложно (поэтому и предпочитают писать в сферических). А центр сферических координат можно взять где угодно. И где бы его ни взять, Вселенная будет выглядеть одинаково. Она же по условию однородна, поэтому все точки равноправны.
Обычно "для наглядности" предлагают посмотреть на раздувающийся воздушный шарик, на котором отмечены точки. Если взять любую из точек за "центр", то остальные удаляются от неё со скоростями, пропорциональными расстояниям до "центра".
По-моему, я рассмотрел все Ваши примеры.
Ну да, какие-то отписки были.
Это не принцип локальности - он ничего не говорит о скорости передачи взаимодействий. Вот уравнения Максвелла - это действительно локальная теория. А в ОТО есть что-то похожее?
Похожее на что?
Электромагнитное и гравитационное поля распространяются со скоростью света (определяемой, естественно, локально). Массивные объекты движутся с меньшей скоростью.
Дело не в наблюдателе, а в принципе локальности и равноправии близнецов. Наблюдатель видит разницу часов после второй встречи близнецов, и эта разница не зависит от этого наблюдателя, она объективна.
Разумеется, разница есть, она объективна, и ОТО позволяет её вычислить. Только возникает она не локально. Мы ведь не можем определить скорость хода часов самих по себе, мы можем только сравнить их с часами, расположенными в другом месте, а эта процедура существенно не локальная (и, вообще говоря, не однозначная).
Думаю, и не только я.

Я уже не раз повторял о необходимости существования локальной возможности, для близнеца, вычислить собственное время неподвижного, в точке старта, наблюдателя.
Видите ли, в СТОшном "парадоксе близнецов" ускорения показывают физическое различие между близнецами. Однако период ускорения может быть относительно коротким, а накопившаяся разница в возрасте - много больше продолжительности ускорения. К тому же, задачу можно сформулировать так, чтобы ускорений как таковых вообще не было. Задачу можно решать разными способами, один из способов (с помощью эффекта Доплера) описан здесь:
http://dxdy.ru/post162688.html#p162688.
Нет, не заметил. В п.105 пишится о разложении поля по степеням

, и рассмотрением только первых двух членов разложения

.
Извините, "внутри массивной сферы" - это никак не"вдали от тел", что обсуждается в § 105.
В п.106 пишется о том, что размеры системы должны быть гораздо меньше, чем длина волны, излучаемые этой системой, гравитационных волн. Наш случай вписывается в эти параметры.
Ну да, если положить

, то наш случай и получится. Однако Вы настаивали на том, что

, и что Вас обманули, подсунув укороченную формулу (которая, тем не менее, оказалась правильной).
Неа. Вот открываю эту страницу, и в который раз вижу, что в формуле стоит не

, а

, и это специально подчёркнуто в начале параграфа. Выражения для интервала там вообще нет, что меня и удивило - пришлось проверить правильность написания интервала для слабых полей. И не зря.
Гы-гы-гы!!! Повеселили. Я всё время говорю студентам: "не придавайте слишком большого значения буквам, буквы могут быть любыми". Здесь имеется просто некоторое различие в терминологии и обозначениях. Или, может быть, Вы будете утверждать, что у Вейнберга совсем другая ОТО, нежели у Ландау с Лифшицем?
P.S. Если Вы покопаетесь в литературе, то обнаружите разные знаки у основных тензоров ОТО - метрического тензора, тензора Римана, тензора Эйнштейна, и даже гравитационная постоянная может оказаться отрицательной. В трёхтомнике Мизнера, Торна, Уилера на внутренней стороне обложки есть большущая таблица, в которой расписано, кто какие знаки использует.
Обозначение

для интервала вводится в главе 2 §§ 1,2.
имеет в виду, что Вейнберг использует термин "собственное время" вместо "интервал". Он, разумеется, не разглядел, что определения-то одинаковые, особенно если учесть, что Вейнберг пользуется системой единиц, в которой скорость света

.



