Уравнение Шредингера в квантовой теории поля

[ИгорЪ]

AlexNew в сообщении #394017 писал(а):

это как ? можете привести в кратце получение ?

Пишем релятивистский лагранжиан свободной частицы. Импульсы удовлетворяют связи, которая при квантовании дает КГ. Разлагаем теперь корень по $c^2$ и вычисляем импульсы $p_t, p_x$ вот они будут удовлетворять связи первого порядка по $t$ после квантования дающей УШ. Квантование это- импульсы превращаем в операторы производных и вводим в.ф., удовлетворяющую уравнению связи. Подробности, хотя и малые, философии такого квантования см. в 1 томе Виттеновского 2-томника по струнам.

-- Пн янв 03, 2011 22:38:29 --

Munin
Я честно пересмотрел всё снова и никакого смысла в 2-пси записи опять не нашел. Нашел слишком много нравоучений вместо физики, и что то мне подсказывает, что вряд ли вы что то можете сказать, отличающееся, от сказаного у Румера с Фетом. Ну и с интерпретацией УД(вижения) как УШ, тоже как то неубедительно.

[Munin]

ИгорЪ в сообщении #394971 писал(а):

Я честно пересмотрел всё снова и никакого смысла в 2-пси записи опять не нашел. Нашел слишком много нравоучений вместо физики, и что то мне подсказывает, что вряд ли вы что то можете сказать, отличающееся, от сказаного у Румера с Фетом.

Я не знаю, что вы называете "сказанным у Румера с Фетом". Но мне крайне удивительно, что вы, читав что-то, и по вашим отзывам, понимая прочитанное, не видите смысла в "2-пси записи". У меня вы не найдёте ничего отличающегося от сказанного в перечисленных мной учебников КТП, и я не считаю это недостатком того, что я могу сказать.

ИгорЪ в сообщении #394971 писал(а):

Ну и с интерпретацией УД(вижения) как УШ, тоже как то неубедительно.

Я не понимаю, какое отношение имеет убедительность к фактам: КТП построена именно так, а не иначе.

Скажите, вы умеете квантовать лагранжеву или гамильтонову систему без связей?

[ИгорЪ]

Munin в сообщении #395050 писал(а):

Скажите, вы умеете квантовать лагранжеву или гамильтонову систему без связей

Читал.

Munin в сообщении #395050 писал(а):

Я не знаю, что вы называете "сказанным у Румера с Фетом".

Дык то что сказано то и называю

Munin в сообщении #395050 писал(а):

У меня вы не найдёте ничего отличающегося от сказанного в перечисленных мной учебников КТП

ни в одном ни нашел! Ткните пальчиком пожалуйста! И чтоб было две пси! Ну и с УД=УШ тоже.

[Munin]

ИгорЪ в сообщении #395167 писал(а):

Читал.

Я не спрашиваю, читали или не читали. Я спрашиваю, умеете квантовать или нет. Потому что под квантованием обычно понимается именно эта процедура, а не то, что вы вычитали у Виттена (достаточно продвинутую концепцию, опирающуюся на эту процедуру, и квантованием называемую только в силу аналогии с этой процедурой).

ИгорЪ в сообщении #395167 писал(а):

Дык то что сказано то и называю

Не прекратите издеваться?

ИгорЪ в сообщении #395167 писал(а):

ни в одном ни нашел! Ткните пальчиком пожалуйста!

Я вам уже перечислял.

[AlexNew]

ИгорЪ писал(а):

Мне удалось так же получить обычное УШ из галилеево инвариантного лагранжиана.

ИгорЪ писал(а):

Пишем релятивистский лагранжиан свободной частицы. Импульсы удовлетворяют связи, которая при квантовании дает КГ.

галилеево или лоренцо инвариантного лагранжиана ??

[ИгорЪ]

AlexNew в сообщении #395384 писал(а):

ИгорЪ писал(а):

Мне удалось так же получить обычное УШ из галилеево инвариантного лагранжиана.

ИгорЪ писал(а):

Пишем релятивистский лагранжиан свободной частицы. Импульсы удовлетворяют связи, которая при квантовании дает КГ.

галилеево или лоренцо инвариантного лагранжиана ??

А что, разве существует галилеево инвариантный лагранжиан релятивистской свободной частицы? Я беру обычный корень из интервала как в ЛЛ2.

-- Ср янв 05, 2011 15:48:04 --

Munin
Вы как жрец, упорно скрывающий знания от народа. Наверное это такой способ возвышения над серой толпой. Вы понимаете, что я искренне не нашел в ваших ссылках ничего! Кроме того, похоже, не один я. Ну не вижу! Вы что, сами ни разу не пропускали, читая книгу в первый, второй и пятый раз, важные моменты, которые сначала таковыми не кажутся?

-- Ср янв 05, 2011 15:50:55 --

А может это всё блеф?

[Munin]

ИгорЪ в сообщении #395621 писал(а):

Munin Вы как жрец, упорно скрывающий знания от народа.

Да. Видимо. Выложил всё, дальше некуда, даже в глотку запихнуть попытался, устал, руки опустил - вот такой я упорно скрывающий знания.

ИгорЪ в сообщении #395621 писал(а):

Вы понимаете, что я искренне не нашел в ваших ссылках ничего!

А вы их искренне читать попытались? Нет же.

Ещё раз. Поставьте рядом две системы. С одной стороны механический осциллятор $L=(d_tq)^2-\omega^2q^2,$ с другой стороны простейшее поле $\mathcal{L}=(\partial_\mu\varphi)^2-m^2\varphi^2.$

У осциллятора одна степень свободы $q.$ У поля $R^3$ степеней свободы $\varphi(x,y,z).$ Раскладывать поле по осцилляторам не будем, важно понимать, что даже без этого значения полевые переменные $\varphi(x,y,z)$ - это такие же величины, как степени свободы механически движущейся системы точек. Хотя они и принимают значение в несколько более абстрактном пространстве "значений поля".

Потом квантуем обе системы. При квантовании состояние системы из точки в пространстве превращается в функцию на всём этом пространстве. Само пространство - пространство степеней свободы. То есть у осциллятора возникает функция $\Psi(q).$ У поля возникает функция $\Psi(\varphi).$ Она задана на бесконечномерном пространстве, и чтобы задать её аргумент, надо задать целиком функцию $\varphi$ на $(x,y,z).$

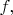
Теперь посмотрим, какие величины мы можем найти из заданного состояния. Чтобы найти среднее физической величины $f,$ надо взять от неё $\langle\Psi|f|\Psi\rangle,$ то есть $f$ определяет билинейную форму на пространстве квантовых состояний. $f|\Psi\rangle$ называем действием оператора $f$ на состояние $\Psi.$

Простейшая физическая величина для осциллятора - это значение его единственной координаты, $q.$ Она превращается в оператор координаты, который обозначается той же буквой. Понятно, как $q$ действует на $\Psi$ в координатном представлении, но очевидно, что как оператор она определена в любом представлении. Для поля аналогичная простейшая величина - это значение отдельной степени свободы поля, то есть отдельной полевой переменной $\varphi(x,y,z).$ Она тоже превращается в оператор, то есть совершенно законна запись $\varphi(x,y,z)\Psi$ - и она имеет смысл независимо от представления.

Взяв несколько операторов от состояния $\Psi,$ можно записать соотношения между тем, что получилось, типа $A\Psi+B\Psi=C\Psi+D\Psi.$ Эти соотношения в классической механике были просто соотношениями между физическими величинами. В квантованном случае - это уравнения на $\Psi$ (например, дифференциальные или интегральные уравнения). Если такое уравнение позволяет целиком вычислить $\Psi,$ то логично его называть уравнением движения. Известно, что уравнение движения можно получить, составив оператор, аналогичный функции Гамильтона в классической механике - гамильтониан, тогда уравнение движения будет иметь вид $i\dot{\Psi}=H\Psi.$ Впрочем, это не единственный способ. Можно брать классическое уравнение движения в разных формах, и получать разные квантовые уравнения движения, совпадающие решениями.

В частности, можно взять результат варьирования лагранжиана. Для осциллятора мы имеем уравнение $d_t^2q+\omega^2q=0.$ Это уравнение напрямую переносится в квантованный случай: $(d_t^2q+\omega^2q)\Psi=0.$ Главная проблема здесь - разобраться, что за оператор будет $d_t^2q$ (оператор второй производной от координаты, или оператор ускорения), но если это сделать, получится уравнение движения, эквивалентное $i\dot{\Psi}=H\Psi.$ Аналогично это можно проделать и для поля. Для классического поля мы имеем $\partial_\mu^2\varphi+m^2\varphi=0,$ для квантованного $(\partial_\mu^2\varphi+m^2\varphi)\Psi=0.$ Оно на вид симметрично по $\mu,$ но на самом деле (пока мы рассматривали представление Шрёдингера) производная по времени и производная по пространственной координате - различно устроенные операторы на $\Psi(\varphi).$ Чтобы их единообразить, можно перейти к представлению Гейзенберга, и тогда наступает всё хорошо.

[Утундрий]

Любопытный поток сознания. А как с такой точки зрения будет выглядеть преставление чисел заполнения, да и вообще - многочастичная задача?

[ИгорЪ]

У меня вышло $d_t^2q=-\omega^2q$ как быть?

-- Чт янв 06, 2011 01:03:14 --

Ну т.е. как УШ то получить из УД?

[Munin]

Утундрий в сообщении #395803 писал(а):

А как с такой точки зрения будет выглядеть преставление чисел заполнения, да и вообще - многочастичная задача?

Не путайте представление чисел заполнения с многочастичной задачей.

Числа заполнения получаются, если поле предварительно разложить по осцилляторам.

ИгорЪ в сообщении #395839 писал(а):

У меня вышло $d_t^2q=-\omega^2q$ как быть?

Решать.

-- 06.01.2011 02:27:24 --

ИгорЪ в сообщении #395839 писал(а):

Ну т.е. как УШ то получить из УД?

Написать УД как классическое уравнение поля. Проанализировать: найти выражение для энергии поля. Проквантовать это поле. После этого выражение $i\dot{\Psi}=H\Psi$ становится УШ для этого квантового поля.

[ИгорЪ]

Munin в сообщении #395859 писал(а):

Решать.

Что решать то? Для осцилятора, подставляя выражение для оператора ускорения, имеем $0\Psi=0$? А вы обещали что будет УШ.

[Munin]

ИгорЪ в сообщении #395905 писал(а):

Для осцилятора, подставляя выражение для оператора ускорения, имеем $0\Psi=0$?

Это выражение вы имеете уже после решения. Подставляйте другое.

ИгорЪ в сообщении #395905 писал(а):

А вы обещали что будет УШ.

Я обещал, что будет уравнение движения.

[Утундрий]

Munin в сообщении #395859 писал(а):

Не путайте представление чисел заполнения с многочастичной задачей.

Числа заполнения получаются, если поле предварительно разложить по осцилляторам.

О связи представления чисел заполнения с многочастичной задачей можно почитать, например, в "КМ" Давыдова (глава, посвященная описанию ансамбля невзаимодействующих фермионов).

[Munin]

Утундрий в сообщении #396000 писал(а):

О связи представления чисел заполнения с многочастичной задачей можно почитать, например, в "КМ" Давыдова (глава, посвященная описанию ансамбля невзаимодействующих фермионов).

Я не отрицаю, что они связаны. Я предлагаю их не путать. В частности, в многочастичной задаче операторов рождения и уничтожения нет. И суперпозиции состояний с разным числом частиц нет.

[ИгорЪ]

Munin в сообщении #395976 писал(а):

Это выражение вы имеете уже после решения.

я ничего не решал!

Munin в сообщении #395976 писал(а):

Подставляйте другое.

Другое какое?

Munin в сообщении #395976 писал(а):

Я обещал, что будет уравнение движения.

Munin в сообщении #395718 писал(а):

Главная проблема здесь - разобраться, что за оператор будет (оператор второй производной от координаты, или оператор ускорения), но если это сделать, получится уравнение движения, эквивалентное

УШ.

А это ваше ?