Otez-osnovatel, а вот понятно ли будет Вам?..

Рассмотрим тогда пространство Лобачевского и конструкцию:

Как было выяснено, этот ряд получается из разложения в ряд Тейлора функции

при

и
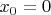
.
Во-первых, мы можем сказать, что отношение длины окружности к диаметру в пространстве Лобачевского всегда больше (или равно) "плоскому"

, также как и отношение катетов в прямоугольном треугольнике

при величине угла

. Поэтому приведенный выше ряд как значение

выражает в пространстве Лобачевского не

, а скажем

или

. То есть мы должны будем записать примерно следующее:
 А во-вторых
А во-вторых, посмотрим повнимательнее на формулу ряда Тейлора:

Мы видим производные, геометрический смысл которых - тангенс угла наклона касательной. А в пространстве Лобачевского касательная будет убегать от графика быстрее, чем в евклидовом, следовательно - пересечет ось

под несколько бОльшим углом. Фактически мы здесь выражаем величину одного угла через величину другого, и я сильно подозреваю, что сумма ряда в пространстве Лобачевского, как и в любом другом,
всегда будет равна

, только вот величина

изменится. Также изменится вид функций тангенса, синуса и, похоже, - всех других. А отношение длины окружности к ее диаметру
всегда будет равно

, просто само значение

будет иным, но мы этого не заметим.
Как видно, два приведенных подхода противоречат друг другу, но какой из них верен? Первый справедлив, если Пи - математический, а второй - эмпирический феномен.



