Вот такая задачка из небезызвестной книжки "Самое полное издание типовых вариантов реальных заданий ЕГЭ, 2010, Математика" Высоцкого, Гущина и Ко (которая на 92 странички):
"Медиана 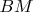 треугольника
треугольника  равна его высоте
равна его высоте  . Найдите угол
. Найдите угол  ."
." (Шестой вариант.)
Так вот, решение достаточно тривиально (в отличие от окружающих С4; что, между прочим, не есть хорошо). Надо просто секундочку поиграться площадями, после чего мгновенно синус равен одной второй, а угол -- соответственно 30 или 150 градусам. Соответственно, ровно те два ответа в той брошюрке и приведены -- а напрасно, между прочим.
Ибо немедленно возникают два встречных предложения.
1) Доказать, что второй вариант фактически не реализуем.
2) Сообщить, что делать ребенку, оказавшемуся в подобной ситуации.
А ребенок, между прочим, непременно попадет в ту ситуацию (если он хоть мало-мальски добросовестен). Поскольку он знает, что это часть С и, следовательно, обязан свои выводы обосновывать. Т.е. не только вычислить возможные значения угла, но и представить примеры, когда те углы достигаются. Ну или опровергнуть.
Ну, с 30-ю градусами -- все, конечно, понятно. А вот со 150-ю -- проблема. Первая же попытка нарисовать картинку наводит на смутные, но глубокие подозрения. Чего-то тут явно не так. Но формально доказать, чего именно -- вовсе не очевидно.
Ну и куды бедному хрестьянину податьси?... Да еще и за ограниченное время?...
------------------------------------------
в порядке пикантности: у них там в этом же варианте еще и ответ на С5 неверен. Какой-то феноменальный вариант.



